Pela situação descrita no enunciado, podemos esboçar as figuras baixo: 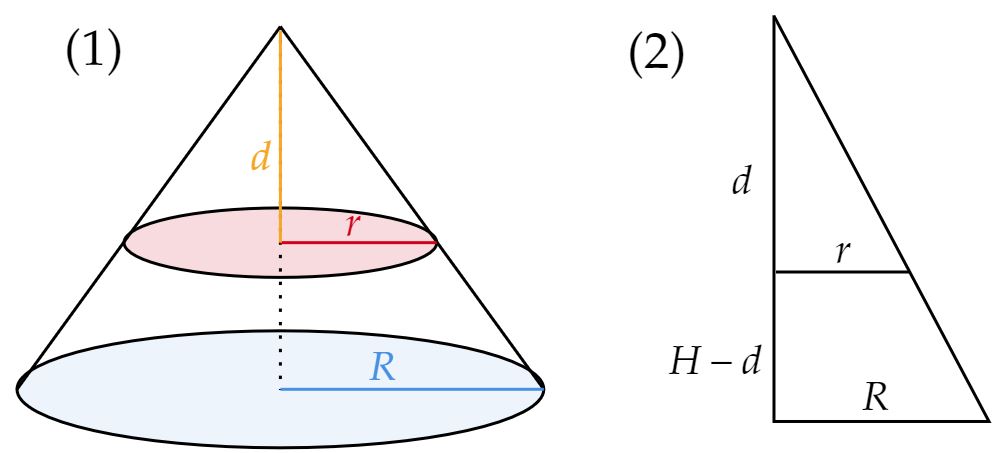Como o volume do tronco é a média geométrica entre os volumes dos cones, têm-se:\begin{matrix} V_{Tronco} = \sqrt{V_{Maior} \cdot V_{Menor}} \end{matrix}Seja $B$ a área da base maior e $b$ a da base menor, então:\begin{matrix} {{\dfrac{(H-d)}{3}}} (B+b + \sqrt{Bb}) =\sqrt{ \left({{\dfrac{H}{3}}} \cdot B \right)\cdot \left( {{\dfrac{d}{3}}} \cdot b\right) } \\ \\ (1-d) \cdot (\pi R^2 + \pi r^2 + \sqrt{(\pi R^2 )(\pi r^2 )} = \sqrt{(\pi R^2)(\pi r^2 )d } \\ \\ (1-d) \cdot \left( {{\dfrac{R}{r}}} + {{\dfrac{r}{R}}} + 1 \right) = \sqrt{d} \ \ \ \color{royalblue}{(3) } \end{matrix}Por uma semelhança de triângulos no item $(2)$, encontra-se: \begin{matrix} {{\dfrac{r}{R} }} = {{\dfrac{d}{H} }} &\therefore& {{\dfrac{r}{R} }} = d \end{matrix}Substituindo o resultado acima em $(3)$: \begin{matrix} (1-d) \cdot \left( {{\dfrac{1}{d}}} + d + 1 \right) = \sqrt{d} \\ \\ d^6 - 3d^3 + 1 = 0 \end{matrix}Resolvendo a equação triquadrática: \begin{matrix} d^3 = {{\dfrac{3 \pm \sqrt{5}}{2}}} &\therefore& d = \sqrt[3]{ {{\dfrac{3 -\sqrt{5}}{2}}} } & \tiny{\blacksquare} \end{matrix}$\color{orangered}{Obs:}$ Atente que, $d <1$ devido $(1-d)$, logo, apenas a raiz negativa satisfaz a condição.\begin{matrix} Letra \ (B) \end{matrix}