A priori, é necessário ter conhecimento do desvio mínimo num prisma - seria bem inviável descobrir isso numa prova. Desse modo, numa súmula, deve-se saber que os ângulos de incidência e emergência do prisma são iguais, assim como os de reflexão, denotemos eles, respectivamente, de $\hat{i}$ e $\hat{r}$. Nesse viés, observe a imagem abaixo: 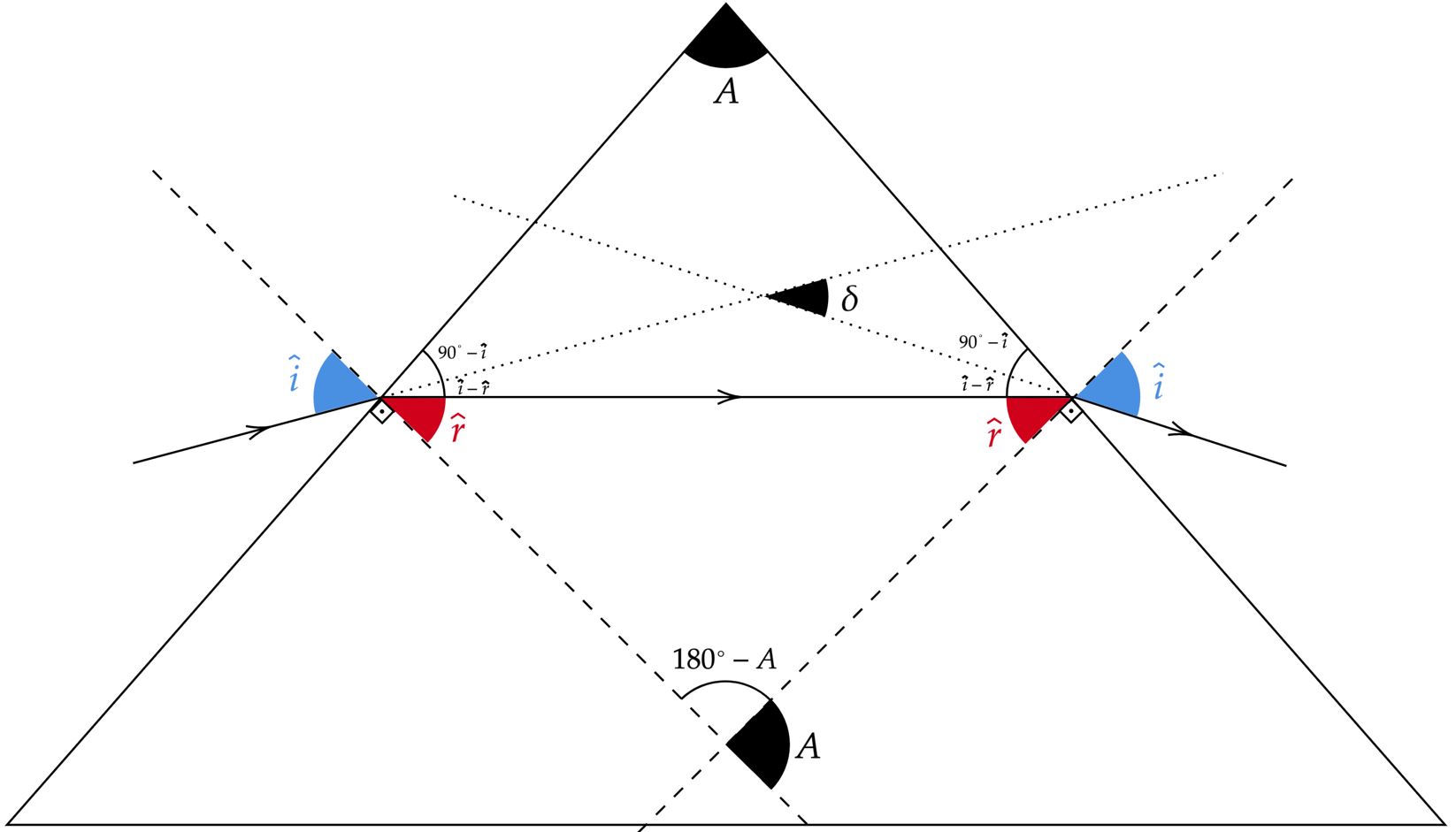Analisando a geometria e trigonometria do problema, existe um resultado particularmente visível:\begin{matrix}(1): \ A = 2 \hat{r} \end{matrix}O resultado $(1)$ pode ser obtido a partir da análise do triângulo inferior, assim como do quadrilátero formado entre os lados do prisma e as retas perpendiculares ao mesmo. Nesse contexto, pode-se aplicar a $\text{Lei de Snell}$ em que: \begin{matrix} \dfrac{\sin{\hat{i}}}{\sin{\hat{r}}} = \dfrac{n}{1} &\Rightarrow& \sin{\hat{i}} = n \cdot \sin{\hat{r}} \end{matrix}Repare que o ângulo $\hat{i}$ não pode exceder $90^{\circ}$, senão teríamos que o raio viria de dentro do prisma (assim como escaparia por dentro), o que certamente é um absurdo, ou seja:\begin{matrix}\sin{\hat{i}} \le 1 &\Rightarrow& n \cdot \sin{\hat{r}} \le 1 &\therefore& \sin{\hat{r}} \le \dfrac{1}{n} \end{matrix}Voltando para a expressão $(1)$, já conseguimos trabalhá-la, veja:\begin{matrix} \hat{r} = \dfrac{A}{2} &\Rightarrow& \sin{\hat{r}} = \sin{\left(\dfrac{A}{2}\right)} \le \dfrac{1}{n} &\therefore& A = 2 \arcsin{(1/n)} &\tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}

Seja $\theta_{1}$ e $\beta_{1}$ o ângulo de incidência e o ângulo de refração do feixe de luz que passa do meio ar para o meio prisma , respectivamente. Denote $\beta_{2}$ e $\theta_{2}$ o ângulo de incidência e o ângulo de refração do feixe de luz que passa do meio prisma para o meio ar , respectivamente. No cenário em que o ângulo $\delta$ é mínimo devemos ter $\beta_{2} < L$ , em que $L$ é o ângulo limite , é importante saber que nesse caso $\theta_{1} = \theta_{2}$ e $\beta_{1} = \beta_{2}$. Sabendo que $ \sin L = \dfrac{n_{ar}}{n} = \sin L = \dfrac{1}{n}$ e $A = \beta_{1} + \beta_{2} $ podemos escrever que $A = \beta_{1} + \beta_{2} = A = 2 \beta_{2} \implies \beta_{2} = \dfrac{A}{2} $ $\therefore$ $\beta_{2} < L \implies \sin \beta_{2} < \sin L = \dfrac{1}{n} > \sin (\frac{A}{2})$ $\therefore$ $\boxed{A < 2 \arcsin (1/n)}$ Portanto, para que esse método possa ser aplicado devemos ter que $A < 2 \arcsin (1/n)$ $\text{Resposta : Alternativa B}$