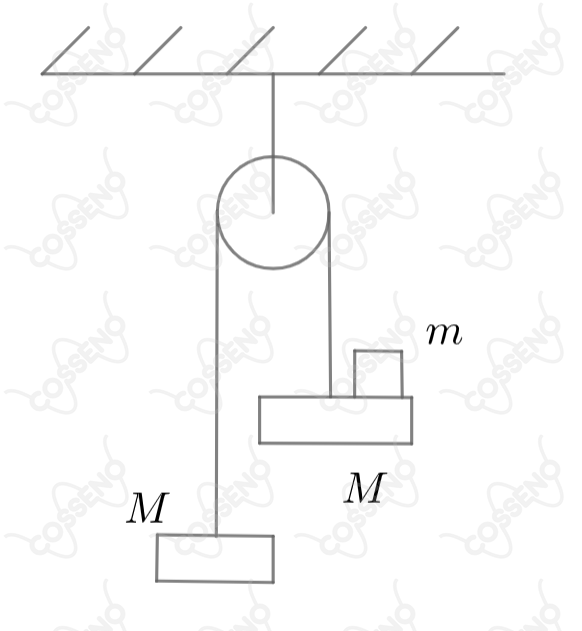
Dois blocos de massa estão unidos por um fio de massa desprezível que passa por uma roldana com um eixo fixo. Um terceiro bloco de massa é colocado suavemente sobre um dos blocos, como mostra a figura. Com que força esse pequeno bloco de massa pressionará o bloco sobre o qual foi colocado?
Isolando os corpos e analisando cada um, podemos denotar a tração da corda de $T$ e a reação de contato entre os dois blocos de $R$, tal que:
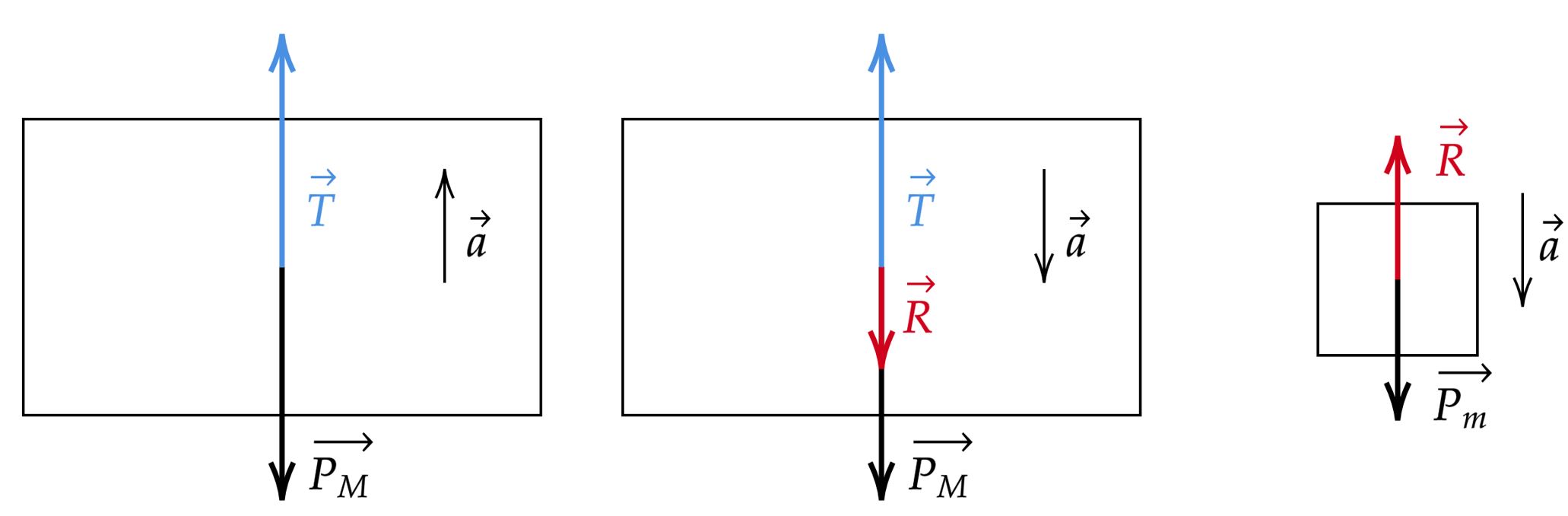Desse modo, têm-se:\begin{matrix}\begin{cases}
M \cdot a &=& T - Mg &(1) \\
M \cdot a &=& R + Mg - T &(2) \\
m \cdot a &=& mg -R &(3)
\end{cases}&\overset{(1)+(2)}{\Rightarrow}& a = \dfrac{R}{2M}
\end{matrix}Substituindo o resultado acima em $(3)$:\begin{matrix}m \cdot \dfrac{R}{2M} = mg -R &\therefore& R = \dfrac{2 \cdot M \cdot m \cdot g}{(2M+m)} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Ampliar Imagem
