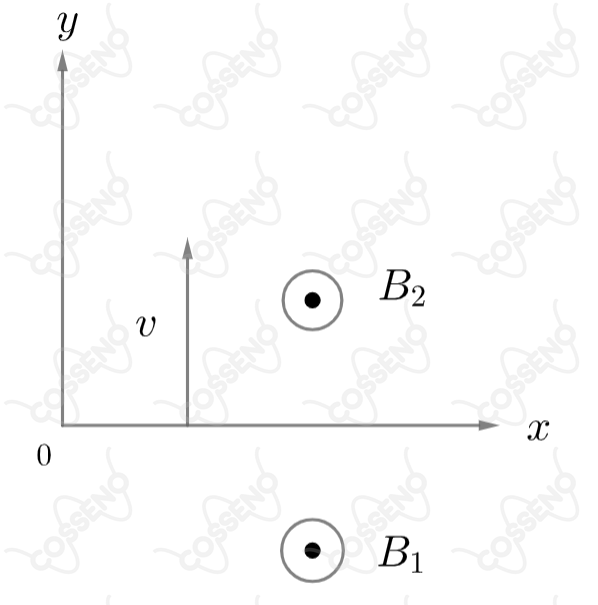
Na figura acima, numa experiência hipotética, o eixo delimita a separação entre duas regiões com valores diferentes de campo de indução magnética, para e para , cujos sentidos são iguais (saindo da página). Uma partícula de carga positiva, , é lançada de um ponto do eixo com velocidade no sentido positivo do eixo . Nessas condições pode-se afirmar que:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Pela regra da mão direita, pode-se dizer que quando a partícula estiver acima do eixo $x \ (y>0)$ a força magnética atuará para direita, analogamente, se a partícula estiver abaixo do eixo $x \ (y<0)$ a força magnética atuará para esquerda. Além disso, perceba que a força magnética fará o papel de resultante centrípeta, proporcionando um movimento curvilíneo.
É intuitivo dizer que, se a força magnética for maior, a curva será menor, proporcionando um menor deslocamento no sentido adotado. Dessa forma, como a força magnética é diretamente proporcional ao campo, podemos marcar a alternativa correta sem esforço.
\begin{matrix} Letra \ (A)
\end{matrix}
Entretanto, vale ressaltar uma solução algébrica, veja: \begin{matrix} |F_M|=|F_{cp}|
&\Rightarrow &B q v = m {{\dfrac{V^2}{R}}} &\therefore& R = {{\dfrac{mV}{Bq}}}
\end{matrix}Após realizar a curva no eixo positivo e voltar do eixo negativo de $y$, temos: \begin{matrix} \Delta x = R_2 - R_1 &\Rightarrow & \Delta x = {{\dfrac{mV}{B_2q}}} - {{\dfrac{mV}{B_1q}}} &\therefore& \Delta x = {{\dfrac{mV}{q}}} \cdot {{(\dfrac{1}{B_2} -\dfrac{1}{B_1} )}}
\end{matrix}Note que, se:
$=> \ \ \ B_1 > B_2:$ Será arrastada para direita
$=> \ \ \ B_2 > B_1:$ Será arrastada para esquerda

