A priori, note que a energia dissipada e consequentemente transformada em calor equivale a energia armazenada no capacitor, esta que pode ser expressa como:\begin{matrix}W = \dfrac{Q^2}{2C} \end{matrix}$• \ \text{Caso I:}$ Este é o mais complexo, a princípio se possui uma associação mista de capacitores, tal que podemos efetuar a seguinte equivalência: 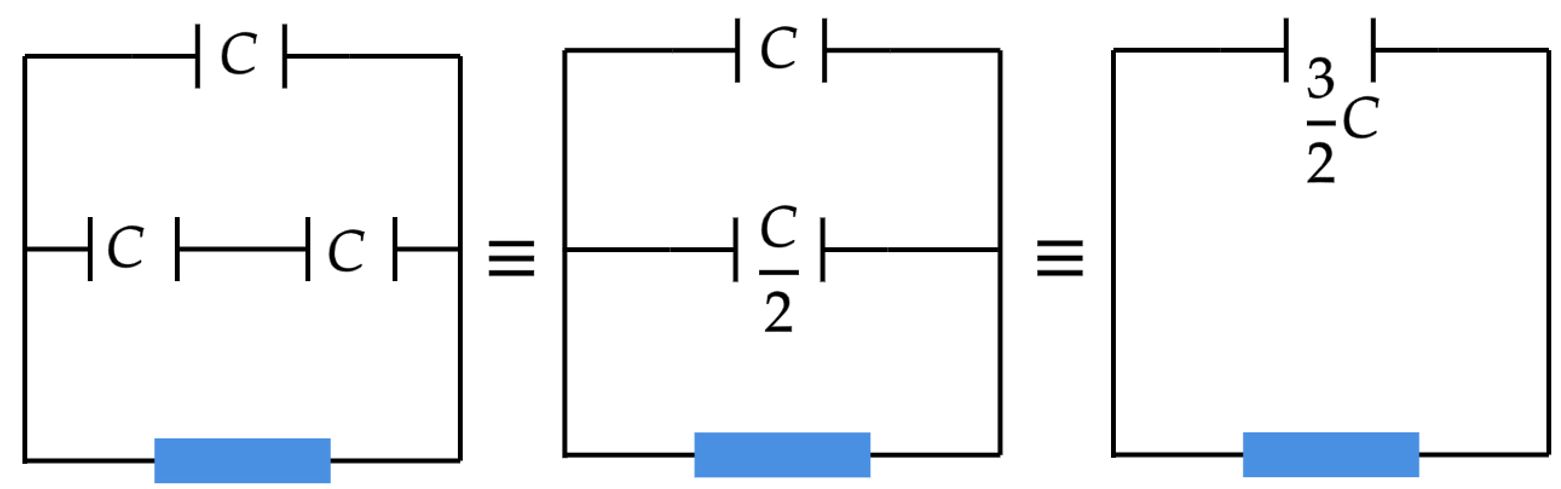Desse modo, temos a capacitância equivalente, contudo, ainda precisamos da carga, para isso, deve-se ter conhecimento do princípio da conservação das cargas, em que podemos analisar a situação inicial abaixo: 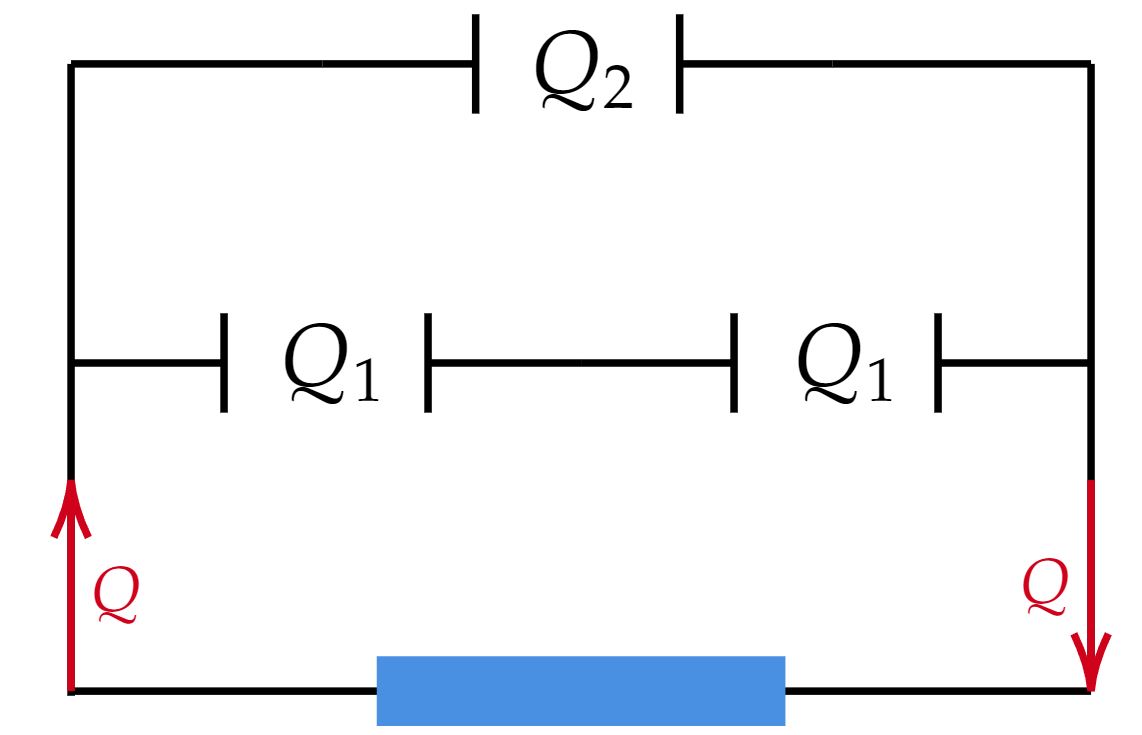$\color{orangered}{\text{Obs:}}$ O fato dos capacitores em série terem cargas iguais é devido a indução total que ocorre. Continuando, podemos equacionar que:\begin{matrix}Q_{eq} = Q_1 + Q_2 &|& \underbrace{2Q_1 + Q_2 = Q}_{\text{conservação da carga}} \end{matrix}Repare que a carga equivalente não é necessariamente a conservação da carga, mas a carga equivalente ao efeito produzido pelo sistema de capacitores. Com isso, ainda é possível se escrever:\begin{matrix} C = \dfrac{Q_2}{\Delta V} &,&\dfrac{C}{2} = \dfrac{Q_1}{\Delta V} &\Rightarrow& Q_2 = 2Q_1 &\therefore& Q_{eq} = \dfrac{3}{4}Q \end{matrix}Por fim, a energia dissipada seria:\begin{matrix} W_I &=& \dfrac{(3Q/4)^2}{2(3C/2)} &=& \dfrac{3}{16} \cdot \dfrac{Q^2}{C} \end{matrix} $• \ \text{Caso II:}$ Neste caso temos apenas um associação em série, tal que:\begin{matrix} C_{eq} = \dfrac{C}{3} &,& Q_{eq} = Q_1 &,& 3Q_1 = Q &\therefore& Q_{eq} =\dfrac{Q}{3} \end{matrix}Então a energia dissipada seria:\begin{matrix} W_{II} &=& \dfrac{(Q/3)^2}{2(C/3)} &=& \dfrac{1}{6} \cdot \dfrac{Q^2}{C} \end{matrix} $• \ \text{Caso III:}$ Já neste, há apenas uma associação em paralelo, em que:\begin{matrix} C_{eq} = 3C &,& Q_{eq} = 3Q_1 &,& 3Q_1 = Q &\therefore& Q_{eq} =Q \end{matrix}Então a energia dissipada seria:\begin{matrix} W_{III} &=& \dfrac{(Q)^2}{2(3C)} &=& \dfrac{1}{6} \cdot \dfrac{Q^2}{C} \end{matrix} $• \ \text{Caso IV:}$ Por fim, o último caso é o mais simples, veja que temos uma carga $Q$ para três capacitores idênticos, ou seja, cada um será carregado com uma carga $Q/3$ no intuito de termos a mesma carga nos três. Agora, basta somar as energias dissipadas por cada um:\begin{matrix} W_{IV} &=& \dfrac{(Q/3)^2}{2C} + \dfrac{(Q/3)^2}{2C} + \dfrac{(Q/3)^2}{2C}&=& \dfrac{1}{6} \cdot \dfrac{Q^2}{C} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}