A priori, perceba que não há atrito, logo, podemos analisar apenas as forças que atuam na horizontal, visto que o peso de cada carrinho irá se igualar com a sua respectiva reação do solo - não havendo efeito horizontal. Nessa perspectiva, vamos denotar a reação entre os carrinhos de $R$, em que já podemos esboçar abaixo: 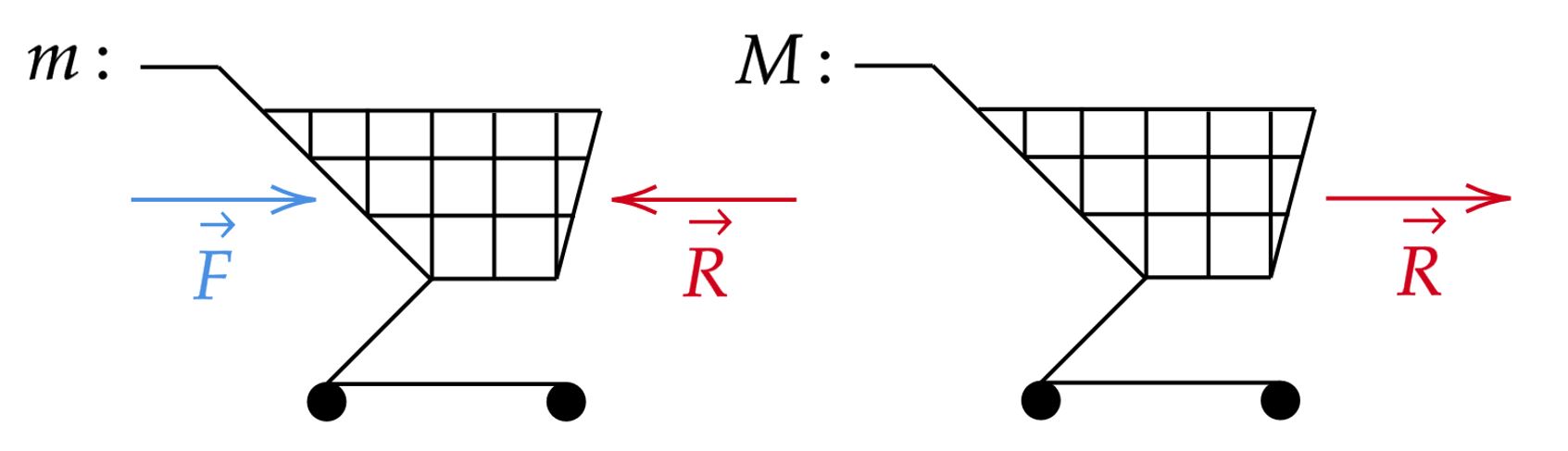Atente que, os carrinhos se movem em conjunto, ou seja, compartilham a mesma aceleração $a$, tal que:\begin{matrix} m \cdot a = F - R &\wedge& M \cdot a = R &\Rightarrow& \dfrac{F-R}{m} = \dfrac{R}{M} &\therefore& R = \dfrac{MF}{(m+M)} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}

$\textbf{Obs : As forças verticais atuantes sobre os carrinhos se}$ $\textbf{anulam , portanto iremos apenas ter uma análise}$ $\textbf{rigorosa das forças na horizontal.}$ Seja $F'$ a força que o carrinho de massa $M$ recebeu , durante a batida estará atuando a força $F$ e $-F'$ sobre o primeiro carrinho enquanto que no segundo carrinho estará atuando sobre ele apenas a força $F'$ , note que durante esse momento a aceleração dos carrinhos são iguais , seja $a$ essa aceleração. Com essas informações podemos escrever as seguintes igualdades: $\begin{cases} F - F' = ma \\ F' = Ma \end{cases}$ $\implies F = ma+Ma =F = a(m + M) \implies a = \dfrac{F}{M + m }$ $\therefore$ $F' = Ma = \boxed{F' =\dfrac{M \cdot F}{M + m}}$ $\textbf{Resposta : Alternativa B}$