Tangenciando externamente a elipse , tal que : considere uma elipse , de eixo maior sobre a reta que suporta o eixo menor de e cujos eixos têm mesma medida que os eixos de . Sabendo que está inteiramente contida no primeiro quadrante, o centro de é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Ajeitando a equação da primeira elipse: \begin{matrix} 9(x^2 - 8x + \color{royalblue}{16}) + 4(y^2 - 6y + \color{royalblue}{9} ) +144 = \color{royalblue}{9\cdot 16} + \color{royalblue}{4\cdot 9} \end{matrix} \begin{matrix}
\epsilon_1: & { \dfrac{(x-4)^2}{2^2} + \dfrac{(y-3)^2}{3^2} }&=& 1
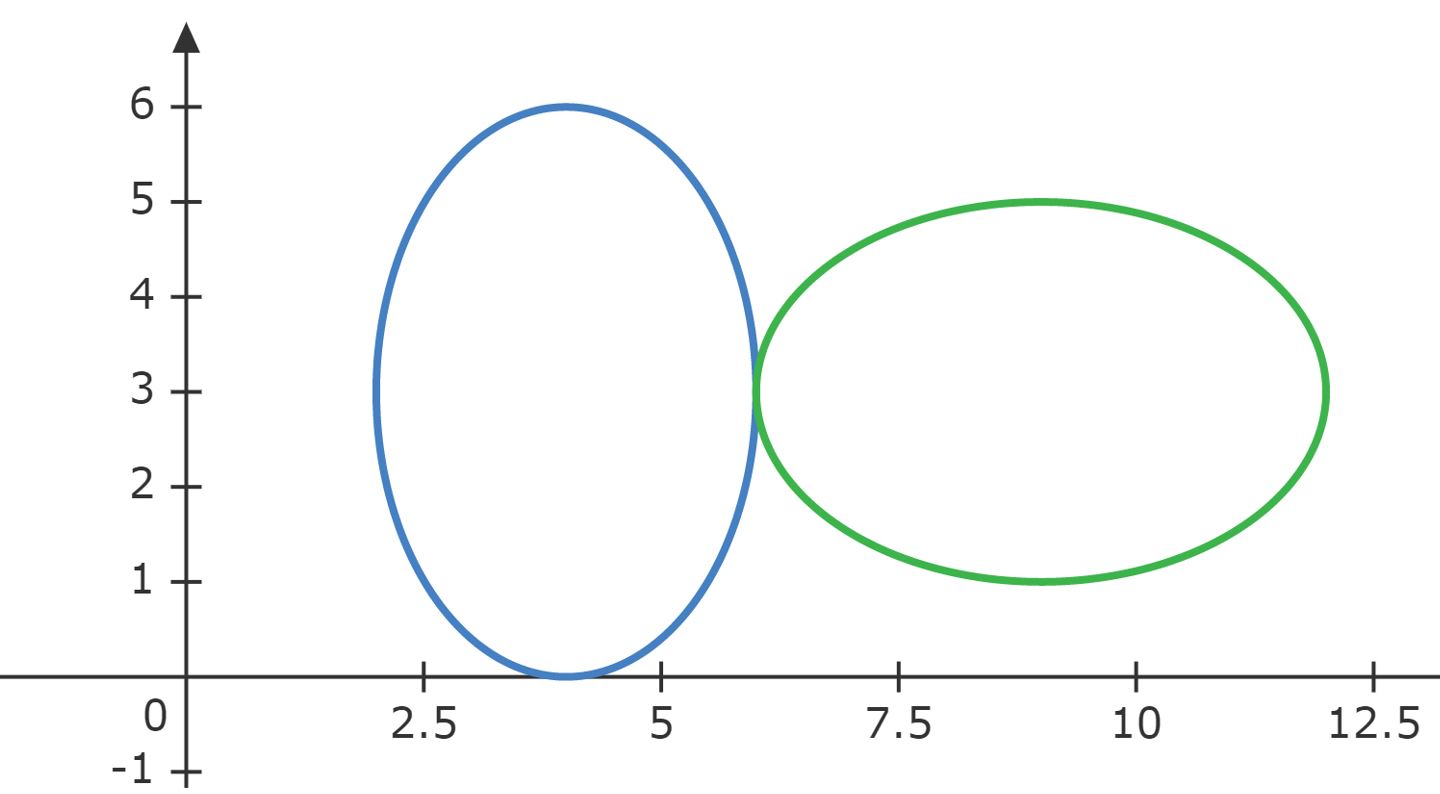
\end{matrix}Com isso, temos o centro $C_1: (4,3)$ da primeira elipse. Atente agora ao enunciado, as elipses possuem eixos de mesma medida, além disso, o eixo maior da segunda elipse tangencia o eixo menor da primeira. Assim, como o eixo menor de $\epsilon_1$ dista duas unidades a direita, e o eixo maior de $\epsilon_2$ dista três unidades a direita, têm-se cinco unidades de distância horizontal entre os centros. Portanto, o centro da segunda elipse está em $C_2: (9,3)$.
$\color{orangered}{Obs:}$ Repare que, o enunciado deixa claro ao dizer que a elipse está no primeiro quadrante, impossibilitando-a de estar a esquerda de $\epsilon_1$.
 \begin{matrix} Letra \ (D)
\end{matrix}
\begin{matrix} Letra \ (D)
\end{matrix}

Ampliar Imagem

