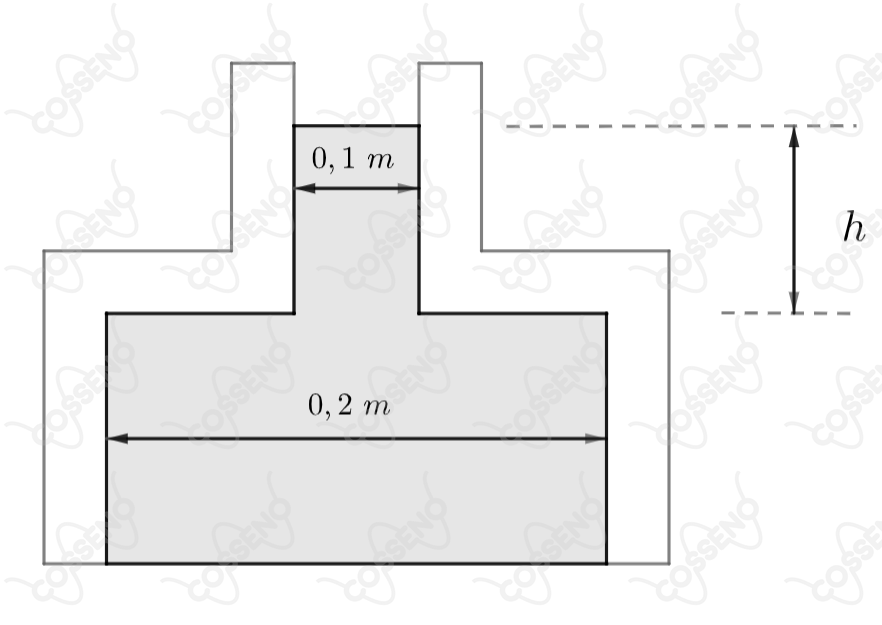
Um recipiente formado de duas partes cilíndricas sem fundo, de massa cujas dimensões estão representadas na figura encontra-se sobre uma mesa lisa com sua extremidade inferior bem ajustada à superfície da mesa. Coloca-se um líquido no recipiente e quando o nível do mesmo atinge uma altura , o recipiente sob ação do líquido se levanta. A massa específica desse líquido é, em :
A priori, podemos pensar na situação em que o líquido é preenchido até o topo da parte cilíndrica maior, veja que o líquido nessa situação exerce pressão apenas nas paredes do cilindro, não sendo capaz de levantá-lo. Nesse contexto, entende-se que o volume de líquido acrescido exerce uma pressão na face superior do cilindro maior, esta pressão pode ser calculada pela $\text{Lei de Stevin}$: \begin{matrix}\Delta p = \rho \cdot g \cdot h &\Rightarrow& \Delta p = 0,5 \rho \end{matrix}Atente que, esta pressão será responsável por uma força $F$ que atua sobre uma área $A$, esta que é a área de uma coroa, a qual pode ser calculada como:\begin{matrix} A = \pi(0,1)^2 - \pi(0,05)^2 &\therefore& A = 2,355 \cdot 10^{-2} \ \pu{m2}
\end{matrix}Agora, repare que a força $F$ deve ser igual ao peso da composição cilíndrica, tal que:\begin{matrix} F = \Delta p \cdot A &|& F = mg &\Rightarrow& 0,5 \rho = \dfrac{mg}{A} &\therefore& \rho \approx 0,85 \ \pu{g/cm3}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}$\color{orangered}{\text{Obs:}}$ $\pu{1 kg/m3 = 10^{-3} g/cm3}$ e $\pi = 3,14$
