Da situação do enunciado, podemos representar como: 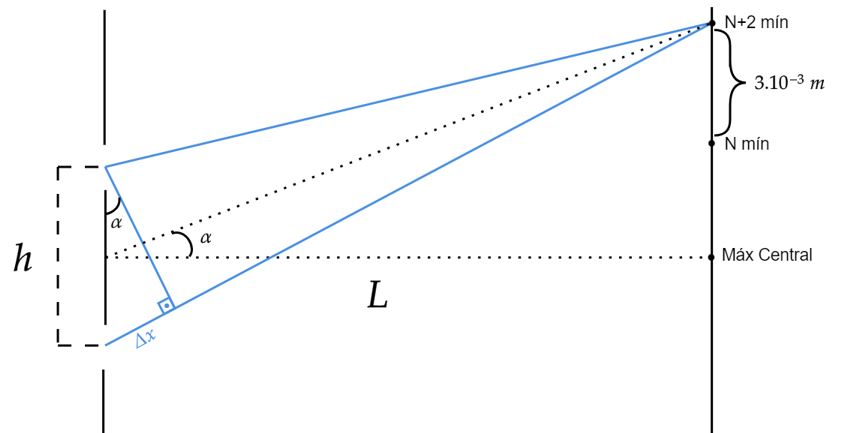$• \ \text{1:}$ Veja que, pela aproximação do enunciado, podemos escrever: \begin{matrix} \sin{\theta} = \tan{\theta} &\Rightarrow& \large{ \frac{\Delta x}{h} = \frac{y}{L}} \end{matrix} $\Delta x$ é a diferença de caminho entre os raios de luz monocromática, dele podemos escrever: $\Delta x = k.\frac{\lambda}{2}$ . Além disso, segundo enunciado, sabemos a separação entre duas franjas escuras vizinhas, arbitramos por $N$ como na imagem acima, assim: \begin{matrix} y_N = \bigg(N\cdot \dfrac{\lambda}{2}\bigg) \cdot {\dfrac{L}{h}} &,& y_{N+2} = \bigg[(N+2)\cdot \dfrac{\lambda}{2} \bigg] \cdot {\dfrac{L}{h}} \end{matrix}Assim, \begin{matrix} \Delta y &=& \lambda \cdot {\dfrac{L}{h}} &=& 3\cdot 10^{-3} \ \pu{ m} &\Rightarrow& \fbox{$\lambda = 5,0 \ \cdot 10^{-7} \ \pu{m}$} \end{matrix}$• \ \text{2:}$ Pela equação fundamental da ondulatória, temos: \begin{matrix} c = \lambda \cdot f &\Rightarrow& \fbox{$f= 6,0 \cdot 10^{14} \ \pu{Hz}$} \end{matrix}$• \ \text{3:}$ Com conhecimento da $\text{Lei de Snell}$: \begin{matrix} { \dfrac{\sin{\theta_1}}{\sin{\theta_2}}} &=& { \dfrac{v_1}{v_2}} &=& { \dfrac{\lambda_1}{\lambda_2}} &=& { \dfrac{n_2}{n_1}} \end{matrix}Então, \begin{matrix} \Large{ \frac{\lambda_1}{\lambda_2}} &=& \Large{ \frac{n_2}{n_1}} &\Rightarrow& \Large{ \frac{\lambda}{5\cdot 10^{-7}}} &=& { \dfrac{1,5}{1}} \end{matrix}\begin{matrix} \fbox{$\lambda = 3,\overline{3} \cdot 10^{-7} \ \pu{m}$} \\ \\ Letra \ (E) \end{matrix}