Resolução ITA 1995 Física

15 ITA 1995 - Física

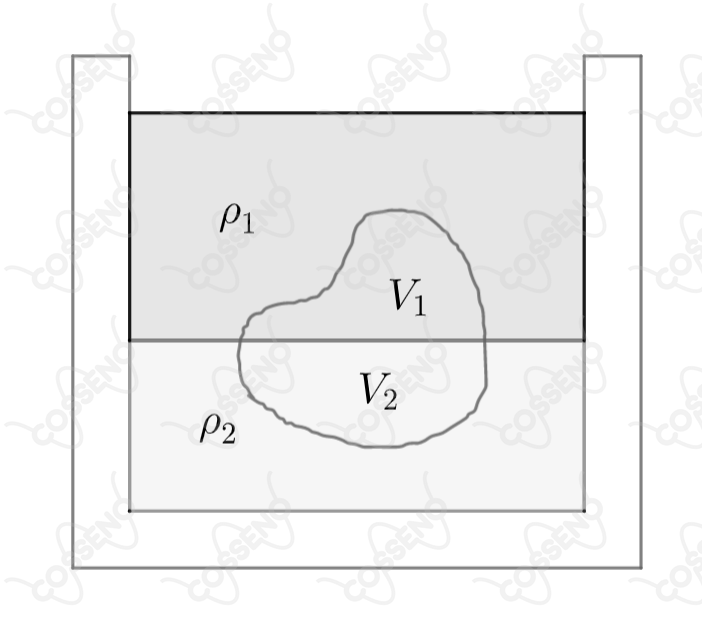
Num recipiente temos dois líquidos não miscíveis com massas específicas $ρ_{1} < ρ_{2}$ . Um objeto de volume $V$ e massa específica $ρ$ sendo $ρ_{1} < ρ < ρ_{2}$ fica em equilíbrio com uma parte em contato com o líquido 1 e outra com o líquido 2 como mostra a figura. Os volumes $V_{1}$ e $V_{2}$ das partes do objeto que ficam imersos em 1 e 2 são, respectivamente:

V_{1} = V (ρ_{1} / ρ); V_{2} = V (ρ_{2} / ρ)

V_{1} = V (ρ_{2} - ρ_{1}) / (ρ_{2} - ρ); V_{2} = V (ρ_{2} - ρ 1) / (ρ - ρ_{1})

V_{1} = V (ρ_{2} - ρ_{1}) / (ρ_{2} + ρ_{1}); V_{2} = V (ρ - ρ_{1}) / (ρ_{2} + ρ_{1})

V_{1} = V (ρ_{2} - ρ) / (ρ_{2} + ρ_{1}); V_{2} = V (ρ + ρ_{1}) / (ρ_{2} + ρ_{1})

V_{1} = V (ρ_{2} - ρ) / (ρ_{2} - ρ_{1}); V_{2} = V (ρ - ρ_{1}) / (ρ_{2} - ρ_{1})

CossenoGPT

Teste gratuitamente agora mesmo!

ITA IIIT 23/12/2021, 12:02

Do enunciado, podemos escrever: \begin{matrix} V &=& V_1 &+& V_2 \end{matrix}Conhecido o Teorema de Arquimedes, e sabido que o volume deslocado é o mesmo que o submerso; como temos líquidos diferentes, há empuxos diferentes, assim:\begin{matrix} P &=& E_1 &+& E_2 \\ \\ m.g &=& \rho_1.V_1.g &+& \rho_2.V_2.g \\ \\ \rho.V.g &=& \rho_1.V_1.g &+& \rho_2.V_2.g \end{matrix}\begin{matrix}{\fbox{$\rho = \dfrac{m}{V}$}} \end{matrix}\begin{matrix} \fbox{$\begin{matrix} V_2.(\rho_2 - \rho) &=& V_1.(\rho - \rho_1) \end{matrix}$} \end{matrix}$•\ V_1 $\begin{matrix} (V - V_1).(\rho_2 - \rho) &=& V_1.(\rho - \rho_1) \end{matrix}\begin{matrix} \fbox{$ V_1 = V \cdot \dfrac{(\rho_2 - \rho) }{(\rho_2 - \rho_1) } $} \end{matrix}$•\ V_2 $\begin{matrix} V_2.(\rho_2 - \rho) &=& (V - V_2).(\rho - \rho_1) \end{matrix}\begin{matrix} \fbox{$ V_2 = V \cdot \dfrac{(\rho - \rho_1) }{(\rho_2 - \rho_1) } $} \end{matrix}\begin{matrix} Letra \ (E) \end{matrix}

Carlos Henrique Prado
19:30 06/04/2023

Por que o empuxo do líquido 1 não tem sinal contrário ao empuxo do líquido 2? Que por sinal daria como resultado a letra d)?

Modo de Edição

0 / 5000

Manual