A figura abaixo mostra um tubo cilíndrico com secção transversal constante de área aberto nas duas extremidades para a atmosfera cuja pressão é . Uma certa quantidade de gás ideal está aprisionada entre dois pistões e que se movem sem atrito. A massa do pistão é desprezível e a do pistão é . O pistão está apoiado numa mola de constante elástica e a aceleração da gravidade . Inicialmente, a distância de equilíbrio entre os pistões é de . Uma massa de é colocada vagarosamente sobre A, mantendo-se constante a temperatura. O deslocamento do pistão para baixo, até a nova posição de equilíbrio, será: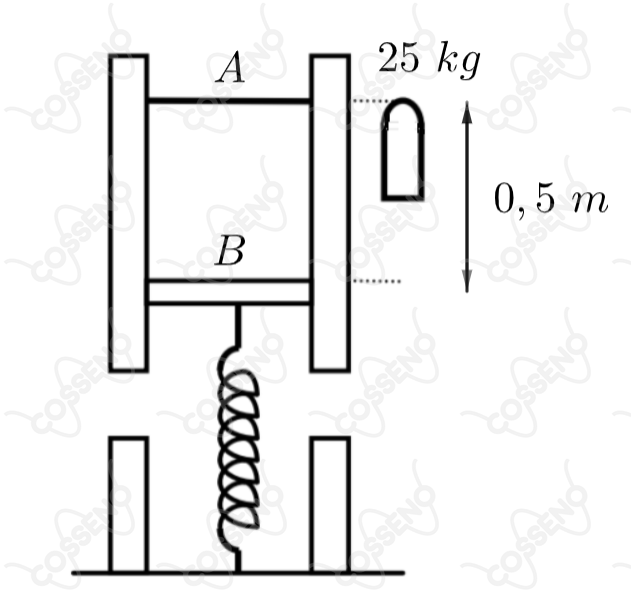
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Adotando o eixo vertical para cima como o sentido das forças positivas, e analisando a situação inicial, com conhecimento que a massa de $A$ é desprezível, a pressão inicial é igual a atmosférica, temos:
\begin{matrix} \large{P_a = \dfrac{F_a}{S}} &\Rightarrow& F_a = 10^3 N
\end{matrix}Ao adicionar a massa de $25 \ \pu{kg}$ no pistão, uma força peso de $250 \ \pu{N}$ vertical para baixo passa atuar no sistema, esse acréscimo de força deve influenciar os dois pistões, exercendo uma nova força $F = F_a + 250$. Dessa forma, sabido que a temperatura é constante, podemos definir a nova distância de equilíbrio entre os pistões, vejamos:
\begin{matrix} PV =cte & \Rightarrow & P_aV_i = PV_f &\Rightarrow& \dfrac{F_a}{S} \cdot (S \cdot 0,5) = \dfrac{F}{S} \cdot (S\cdot d) &\therefore& \fbox{$d = 0,4 \ \pu{m}$}
\end{matrix}Agora, precisamos saber como o pistão $B$ age conforme esse acréscimo de força, isto é, o quanto ela desloca o pistão:
\begin{matrix} Fel = K\cdot x = -250 &\therefore& \fbox{$x = -0,1 \ \pu{m}$}\end{matrix}
$\color{orangered}{Obs:}$ O sinal negativo apenas informa que o pistão desceu, não se esqueça que a força é vertical para baixo.
Analisando nossos resultados, podemos dizer que o pistão $B$ desceu $0,1\pu{m}$, isto é, aumentou-se o volume do sistema. Entretanto, segundo nossa nova distância de equilíbrio entre os pistões, eles devem estar separados de $0,4\pu{m}$. Portanto, $\fbox{o pistão $A$ deve se deslocar exatamente $0,2\pu{m}$ para baixo}$, assim, compensando o deslocamento que ocorreu em $B$.\begin{matrix} Letra \ (D)
\end{matrix}

