A figura ilustra um carrinho de massa percorrendo um trecho de uma montanha russa. Desprezando-se todos os atritos que agem sobre ele e supondo que o carrinho seja abandonado em , o menor valor de para que o carrinho efetue a trajetória completa é: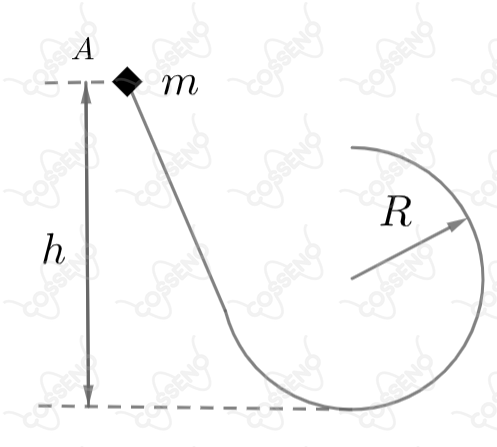
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Encontrar o menor valor de $h$ significa que o carrinho fará o loop na condição de iminência: quando ele estiver prestes a cair e sua normal chegar numericamente próxima de $0$. Assim, vejamos:\begin{matrix}F_{cp} = P + N &\Rightarrow& m \cdot {{\dfrac{V^2}{R}}} =m \cdot g + 0 &\therefore& V^2 = R \cdot g
\end{matrix}Como o sistema é conservativo, visto que não existe atrito ou qualquer outra resistência, podemos escrever: \begin{matrix}E_{M_i} =E_{M_f} &\Rightarrow& m\cdot g\cdot h = m\cdot g\cdot (2R) + {{\dfrac{m\cdot V^2}{2}}} &\therefore& \fbox{$h = \dfrac{5R}{2}$}
\end{matrix}\begin{matrix}Letra \ (B)
\end{matrix}

19:23 16/03/2023
Luiza, acho que o carrinho na iminência de cair tem energia potencial gravitacional. Por isso, mg(2R). Como ele está no topo da circunferência, 2R é a altura que ele se encontra do "solo".

16:42 16/01/2023
Ótima resolução, porém ainda me restou uma dúvida. Por que a altura do lado direito da equação é igual a 2R?

06:16 24/03/2023
é considerada a medida do diâmetro da circunferência. Se o raio é R, o diâmetro (altura do carrinho em relação ao solo) será de 2R.

