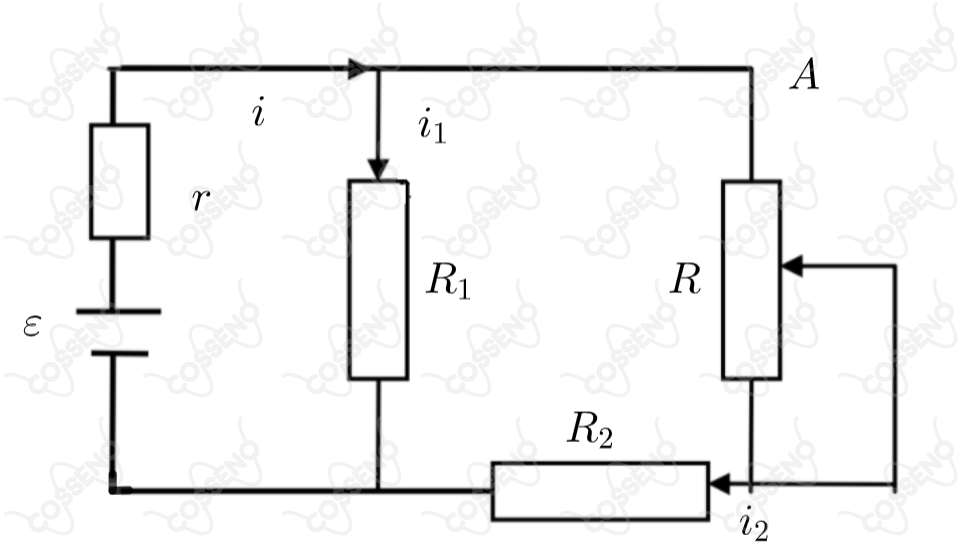
No circuito mostrado acima na figura a força eletromotriz e sua resistência interna são respectivamente e . e são duas resistências fixas. Quando o cursor móvel da resistência se move para A, a corrente em e a corrente em variam, respectivamente, da seguinte forma:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Inicialmente, a situação trata de um reostato, isto é, ao movimentar o cursor para $A$, estaremos diminuindo a resistência do ramo, pois a corrente passará diretamente até $R_2$. Dessa forma, comecemos fazendo a associação em paralelo da imagem: \begin{matrix} {{\dfrac{1}{R_{eq}}}} = {{\dfrac{1}{R_{1}}}} + {{\dfrac{1}{R_{2} + R}}} &\Rightarrow& R_{eq} = {\dfrac{1}{{\dfrac{1}{R_{1}}} + {\dfrac{1}{R_{2} + R}}}}
\end{matrix}Atente que, se $R$ diminui, $R_{eq}$ também diminui, e vice-versa. Nessa perspectiva, precisamos saber como isso influencia as correntes $i_1$ e $i_2$; continuando, conhecida a resistência equivalente, pela $\text{Primeira Lei de Ohm}$: \begin{matrix} \varepsilon = (r + R_{eq}).i &\therefore& i= {\dfrac{\varepsilon}{ (r + R_{eq})}} &,& i = i_1 + i_2
\end{matrix}Constata-se então que, ao diminuir $R_{eq}$, aumentamos a intensidade da corrente $i$, esta responsável por $i_1$ e $i_2$.
Repare agora em $i_1$, novamente, pela $\text{Primeira Lei de Ohm}$: \begin{matrix} \Delta V = R_1.i_1 &,& \Delta V = \varepsilon - r.i &\Rightarrow& i_1 = {\dfrac{\varepsilon - r.i }{R_1}}
\end{matrix}Assim, o aumento de $i$ caracteriza o decréscimo de $i_1$, o que consequentemente acarreta o aumento de $i_2$. \begin{matrix}Letra \ (C)
\end{matrix}


