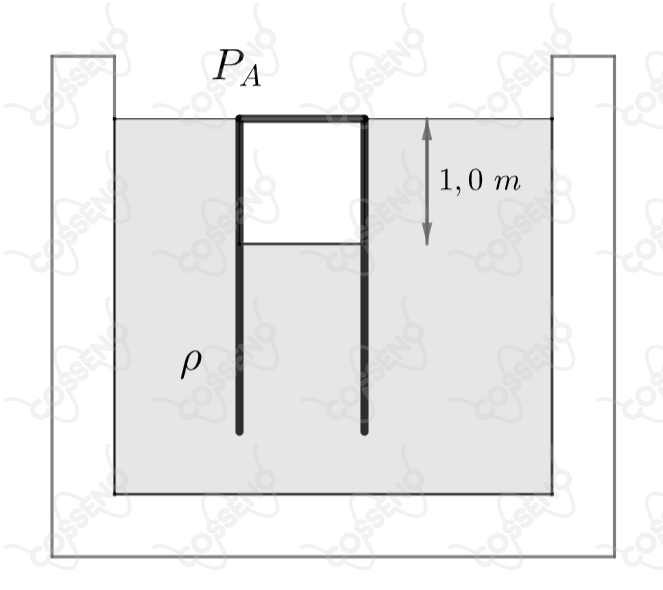
Um tubo cilíndrico de secção transversal constante de área fechado numa das extremidades e com uma coluna de ar no seu interior de encontra-se em equilíbrio mergulhado em água cuja massa específica é com o topo do tubo coincidindo com a superfície (figura abaixo). Sendo pressão atmosférica e a aceleração da gravidade, a que distância deverá ser elevado o topo do tubo com relação à superfície da água para que o nível da água dentro e fora do mesmo coincidam?
CossenoGPT
Teste gratuitamente agora mesmo! 
A priori, pode-se encontrar a pressão exercida pelo ar dentro do tubo, para isso, deve-se ter conhecimento da $\text{Lei de Stevin}$ e suas consequências, mais precisamente que podemos traçar uma linha de nível isobárica no sistema. Veja o esboço da situação abaixo:
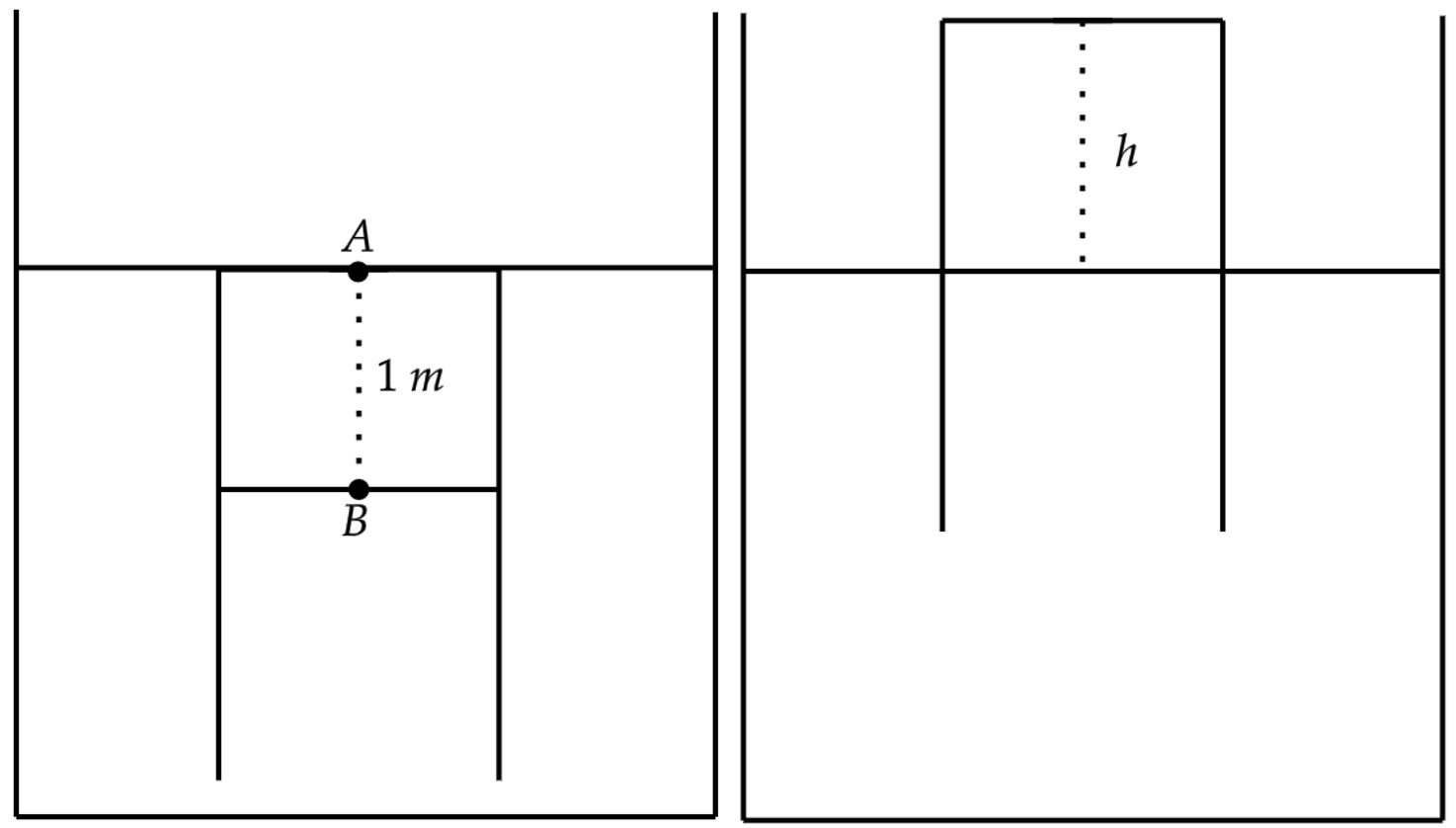Aplicando o a lei de Stevin, têm-se:\begin{matrix} P_B - P_A = \rho \cdot g \cdot 1 &\therefore& P_B = 11 \cdot 10^4 \ \pu{Pa}
\end{matrix}Agora, precisamos assumir que o ar dentro do tubo se comporta como um gás ideal, além disso, deve-se assumir que todo processo é isotérmico, ou seja:\begin{matrix} P \cdot V = cte &|& P_B \cdot (S \cdot 1) = P_A \cdot (S \cdot h) &\Rightarrow& h = \dfrac{P_B}{P_A} &\therefore& h \approx 1,1 \ \pu{m} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Ampliar Imagem
