Segundo enunciado a pirâmide é triangular regular, isto é, uma de suas faces - a base - apresenta um triângulo equilátero de lado $a$. Nesse perspectiva, denotemos as demais arestas de $b$, em que os triângulos das faces apresentem uma altura $h$, enquanto a altura do triângulo equilátero será $3x$. Desse modo, queremos começar encontrando a altura $h$ em função de $a$, então: 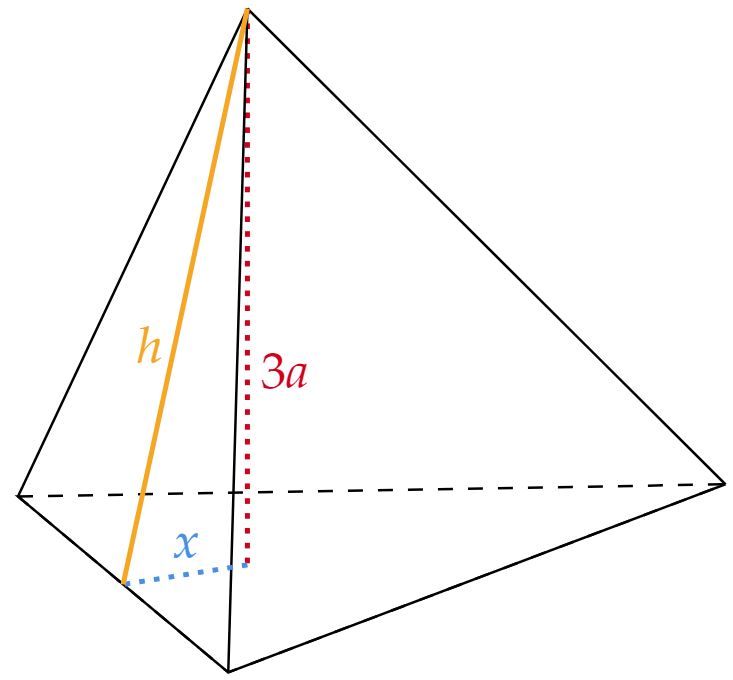\begin{matrix} 3x = {{\dfrac{a\sqrt{3}}{2}}} &\therefore& x = {{\dfrac{a\sqrt{3}}{6}}} \end{matrix}Aplicando Pitágoras: \begin{matrix} h^2 = (3a)^2 + x^2 &\therefore& h = {{\dfrac{a\sqrt{327}}{6}}} \end{matrix}Com isso, a área total da pirâmide:\begin{matrix} A_{Total} = A_{Base} + 3 \cdot A_{Faces} &\Rightarrow& A_{Total} = {{\dfrac{a^2\sqrt{3}}{4}}} + 3\cdot \left(2\cdot {{\dfrac{a\cdot h}{4}}}\right) \end{matrix}Portanto, \begin{matrix} A_{Total} = {{\dfrac{a^2\sqrt{3} (1 + \sqrt{109})}{4}}} & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (E) \end{matrix}