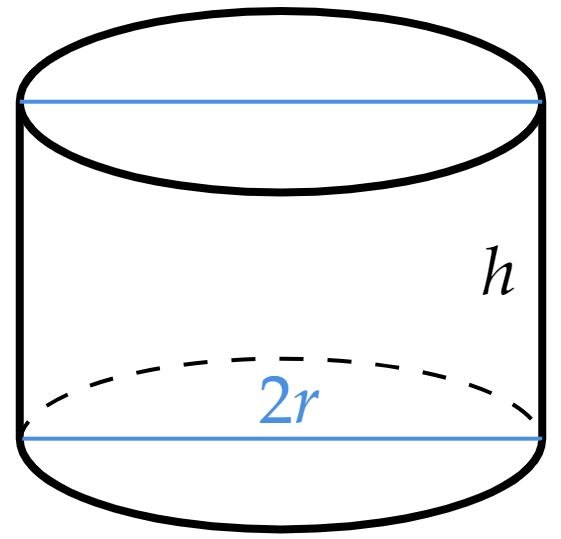
O raio de um cilindro de revolução mede . Sabe-se que a área da base do cilindro coincide com a área da secção determinada por um plano que contém o eixo do cilindro. Então, a área total do cilindro, em , vale:
CossenoGPT
Teste gratuitamente agora mesmo! 
Pela situação descrita no enunciado: \begin{matrix} A_{\text{base}} = A_{\text{secção}} &\Rightarrow& \pi r^2 = (2r) \cdot h &\therefore& h = {{\dfrac{3}{4}}}\pi
\end{matrix}Com isso, a área total do cilindro: \begin{matrix} A_T = A_{\text{lateral}} + 2A_{\text{base}} =
(2\pi r \cdot h) + 2( \pi r^2) \\ \\ A_T = {{\dfrac{9\pi}{4}}}(\pi + 2) \ \ \tiny{\blacksquare}
\end{matrix}
\begin{matrix}Letra \ (B)
\end{matrix}
Ampliar Imagem
