Planificando a situação descrita, e denotando o raio da esfera de $R$, têm-se: 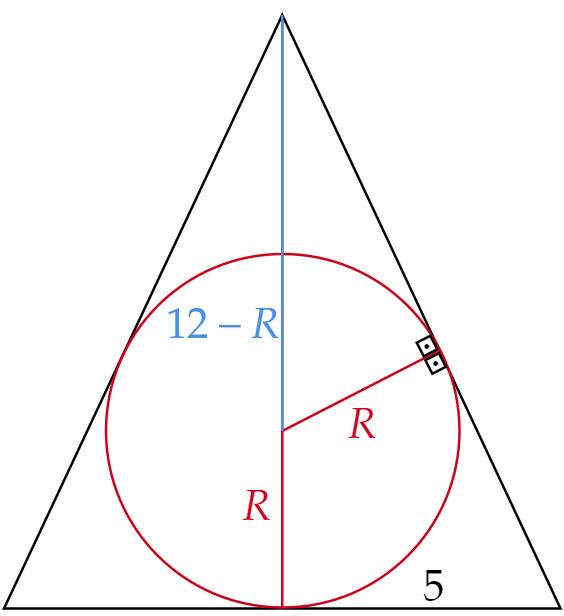Nessa perspectiva, seja a geratriz do cone igual $g$, por Pitágoras, encontra-se: \begin{matrix} g^2 = 5^2 + 12^2 &\therefore& g = 13 \ \pu{cm} \end{matrix}Por fim, a partir de uma semelhança de triângulos: \begin{matrix} {{\dfrac{12-R}{R}}} = {{\dfrac{g}{5}}} &\therefore& R ={{\dfrac{10}{3}}} \ \pu{cm} & \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (A) \end{matrix}