Um elétron (massa e carga ) com uma velocidade penetra na região de um campo magnético homogêneo de indução magnética perpendicularmente à direção do campo, como mostra a figura. A profundidade máxima de penetração do elétron na região do campo é: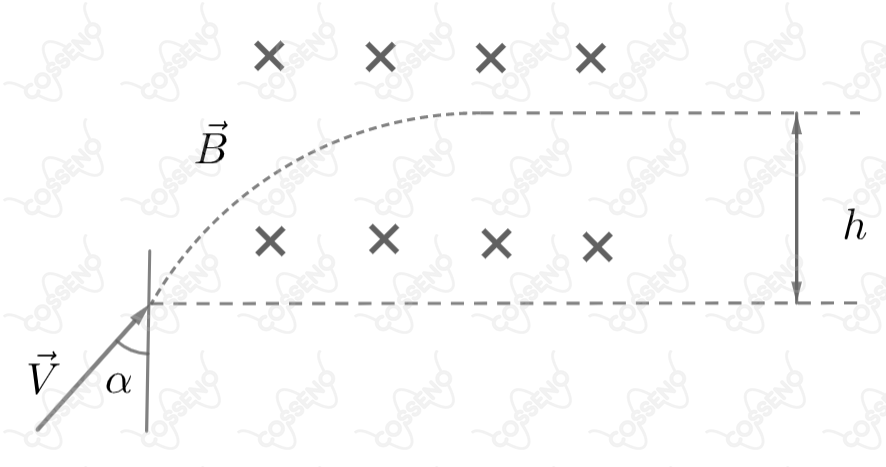
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, é possível perceber pela imagem que o elétron faz um movimento curvilíneo até atingir um movimento linear de altura $h$. Dessa forma, ao analisar a imagem é visível que o raio da curva é maior que $h$, trace uma perpendicular a $V$ e perceba que $R >h$. Ademais, é sabido que nossa força magnética atuará como resultante centrípeta, logo:
\begin{matrix} |F_{cp}|=|F_M| &\Rightarrow& m \cdot {{\dfrac{V^2}{R}}} = B \cdot e \cdot V &\therefore&R = {{\dfrac{m \cdot V}{B \cdot e}}}
\end{matrix}Pela geometria do problema, você deve encontrar: \begin{matrix} h = R \cdot (1-\sin{\alpha}) &\Rightarrow& \fbox{$h = \dfrac{m \cdot V}{B\cdot e}\cdot (1-\sin{\alpha})$}
\end{matrix}\begin{matrix} Letra \ (B)
\end{matrix}

