Denotemos as cargas iniciais de $q_1$ e $q_2$, segundo enunciado, o valor dessas cargas será: \begin{matrix}q_1 = C_1.\Delta V_1 &\Rightarrow& q_1 = 200 \ \mu C &&\\ q_2 = C_2.\Delta V_2 &\Rightarrow& q_2 = 800 \ \mu C \end{matrix}Com isso, após desligarmos as baterias, teremos uma situação como abaixo: 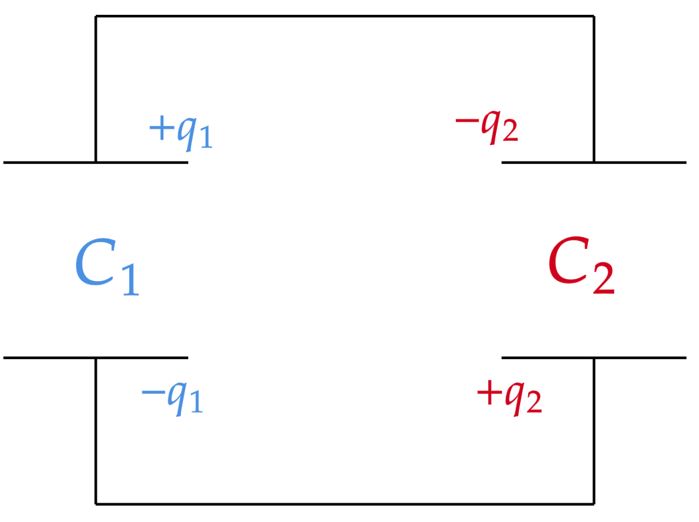Atente que, temos uma associação em paralelo, logo: \begin{matrix} C_{eq} =C_1 + C_2 &,& |Q_{eq}| = |q_2 - q_1| = |q_1 - q_2| \\ \\ C_{eq} =3 \ \mu F && Q_{eq} = 600 \ \mu C \end{matrix}Dessa forma, a diferença de potencial nos capacitores: \begin{matrix} Q_{eq} = C_{eq}.\Delta V_{eq} &\therefore& \fbox{$\Delta V_{eq} = 200 \ V$} \end{matrix}Por fim, analisando a perda da energia armazenada nos capacitores, no inicio, tínhamos: \begin{matrix} E_1 = {\large{\frac{\Delta V_1^2 \ . \ C_1}{2}}} &\Rightarrow& E_1 = 2.10^4 \ \mu J \\ E_2 = {\large{\frac{\Delta V_2^2 \ . \ C_2}{2}}} &\Rightarrow& E_2 = 16.10^4 \ \mu J \end{matrix}Já no final: \begin{matrix} E_{f} = {\large{\frac{\Delta V_{eq}^2 \ . \ C_{eq}}{2}}} &\Rightarrow& E_{f} = 6.10^4 \ \mu J \end{matrix}Então a perda de energia será: \begin{matrix} |\Delta E |= |E_f - (E_1 + E_2)| &\therefore& \fbox{$ |\Delta E| = 0,12 \ J $} \end{matrix}\begin{matrix} Letra \ (C) \end{matrix}