Com conhecimento do trabalho realizado pela força de atrito num plano inclinado, a questão fica relativamente simples. Caso contrário, seria interessante fazer esta análise para um plano arbitrário como abaixo: 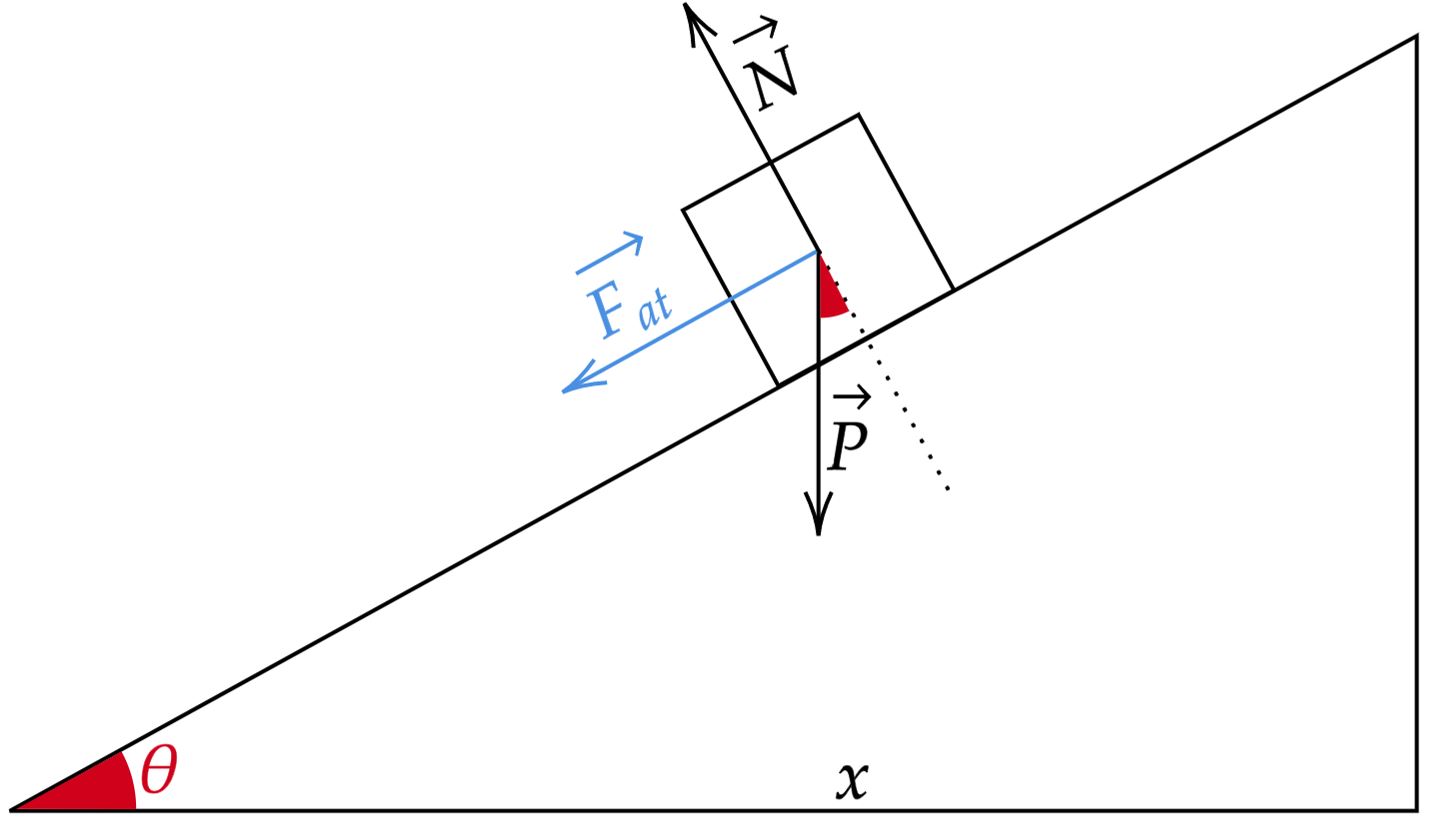Pensando nas forças que atuam no bloco, podemos escrever: \begin{matrix} F_{at} = N \cdot \mu &,& N = P \cdot \cos{\theta} &\therefore& F_{at} = P \cdot \mu \cdot \cos{\theta} \end{matrix}Admitindo que a rampa possua um comprimento $d$, o trabalho que a força de atrito teria de realizar é: \begin{matrix} W_{F_{at}} = F_{at} \cdot d &|& \cos{\theta} = \dfrac{x}{d} &\therefore& \boxed{W_{F_{at}} = \mu \cdot P \cdot x} \end{matrix}Analisando o resultado obtido, nota-se que o trabalho da força de atrito num plano inclinado é uma relação entre o peso, o coeficiente de atrito e a distância horizontal. Nesse contexto, por simetria, não é difícil dizer que na situação do enunciado temos:\begin{matrix} T_1 &=& T_2&=& T_3 \end{matrix}Agora, pensando no $\text{teorema do trabalho-energia}$, têm-se entre os pontos $A$ e $B$: \begin{matrix} T_{i} + W_P = \Delta E_c &|& W_P = 0 \ \pu{J} &\therefore& T_i = \Delta E_c \end{matrix}Como os trabalhos realizados são iguais, consequentemente:\begin{matrix} V_{b_1} &=& V_{b_2} &=& V_{b_3} \end{matrix}\begin{matrix}Letra \ (E) \end{matrix}