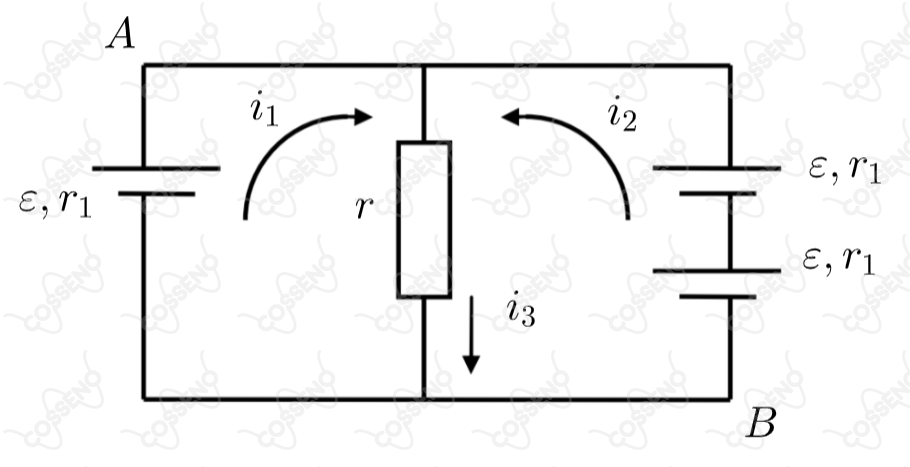
Baseado no esquema a seguir onde , e as correntes estão indicadas, podemos concluir que os valores de , , e () são, respectivamente:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Admitindo correto o sentido das correntes, podemos escrever para malha em que passa $i_1$: \begin{matrix} r_1.i_1 - \varepsilon + r.i_3 = 0 &\Rightarrow& i_1 + 10i_3 = 2
\end{matrix}Já na malha em que se passa $i_2$, \begin{matrix} 2(r_1.i_2) - 2(\varepsilon) + r.i_3 = 0 &\Rightarrow& 2i_2 + 10i_3 = 4
\end{matrix}Além de claro, \begin{matrix} i_3 = i_1 + i_2
\end{matrix}Forma-se assim um pequeno sistema, veja: \begin{matrix}
\begin{cases} i_1 &+& 10i_3 &=& 2 \\ 2i_2 &+& 10i_3 &=& 4 \\ i_1 &+& i_2 &=& i_3
\end{cases} &\therefore& \fbox{$ i_1 = -0,50 \ A$} &,& \fbox{$ i_2 = 0,75 \ A$} &,& \fbox{$ i_3 = 0,25 \ A$}
\end{matrix}$\color{orangered}{Obs:}$ Nota-se que o sentido adotado para $i_1$ foi equivocado, isto é, o contrário.
Por fim, a $d.d.p$ entre os pontos $B$ e $A$, vide $\text{Lei de Ohm Generalizada}$: \begin{matrix}V_B-V_A = -\varepsilon +r_1.i_1 &\therefore& \fbox{$ V_B -V_A = -2,5 \ V $}
\end{matrix}\begin{matrix} Letra \ (D)
\end{matrix}

