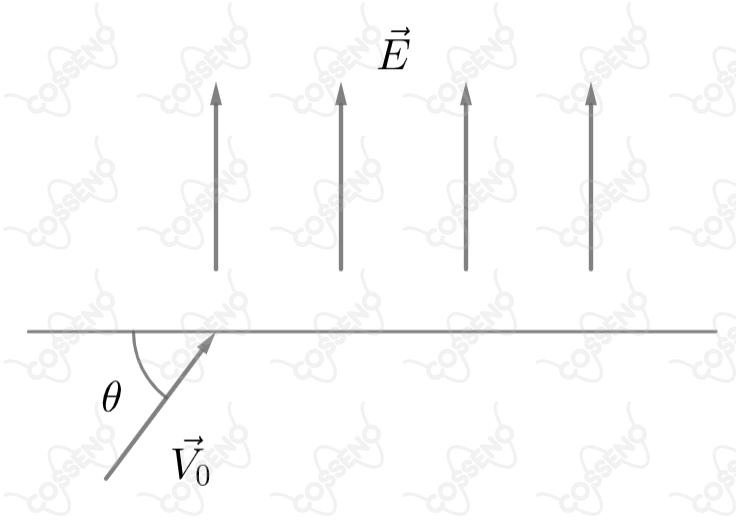
Numa região onde existe um campo elétrico uniforme dirigido verticalmente para cima, penetra um elétron com velocidade inicial segundo uma direção que faz um ângulo com a horizontal como mostra a figura. Sendo a massa do elétron e a carga podemos afirmar que:
O elétron tem carga negativa e o campo elétrico está voltado para cima, assim, a força elétrica será direcionada para baixo:
\begin{matrix} |F_r| = |F_e|&\Rightarrow& m\cdot a = E\cdot e &\Rightarrow & a = \dfrac{E \cdot e}{m}
\end{matrix}Podemos decompor a velocidade do elétron ao entrar no campo em:\begin{matrix} V_y = V_0 . \sin{\theta} &,& V_x = V_0 \cdot \cos{\theta}
\end{matrix}Calculando o tempo de queda do elétron:
\begin{matrix} 0 = V_y + (-a)\cdot t &\Rightarrow& t = \dfrac{V_0 \cdot \sin{\theta}}{a} &\Rightarrow& t = \dfrac{m \cdot V_0 \cdot \sin{\theta}}{E\cdot e}
\end{matrix}
Agora, basta substituir os valores e aproximar o resultado:
\begin{matrix} \fbox{$ t \approx 1,14\cdot 10^{-8}$} \\ \\ Letra \ (A)
\end{matrix}
$\color{orangered}{Obs:}$ A aproximação pode ser visualmente complicada, mas perceba que ao analisar as demais alternativas, todas passam longe, deixo a ideia de cada:
$• \ B:$ Aplique $A = V_x. t$
$• \ C:$ Já encontramos no início
$• \ D:$ Não, será para baixo
$• \ E:$ Aplique Torricelli
