Na figura, e são duas fontes pontuais iguais, de luz monocromática em fase. A tela está colocada a de distância. Inicialmente e estavam encostadas. Afastando-se de de observou-se no ponto A um primeiro escurecimento quando . Considerando a aproximação para , a distância para o terceiro escurecimento será: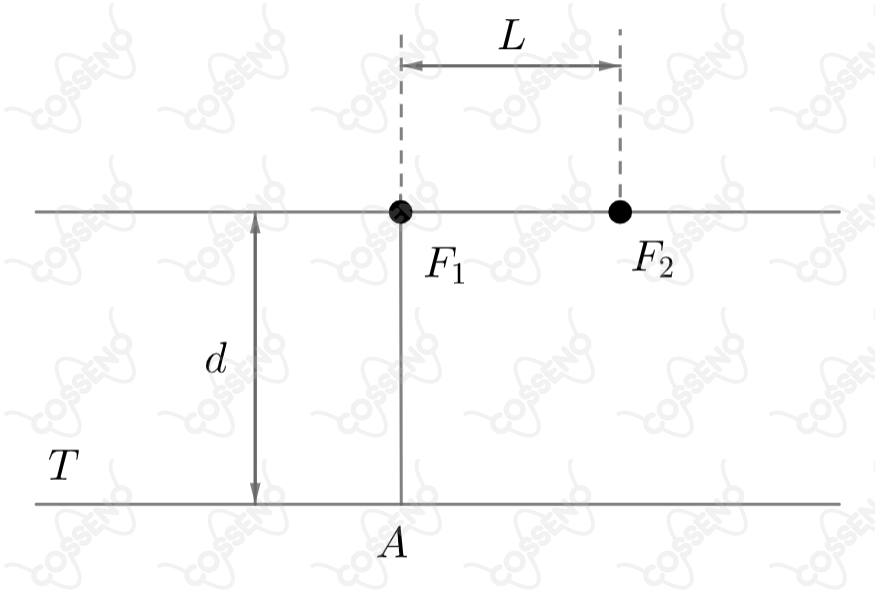
CossenoGPT
Teste gratuitamente agora mesmo! 

Segundo enunciado, podemos esboçar a situação como na figura abaixo, $F_3$ será a nova posição de $F_2$, aquela que proporcionará o terceiro escurecimento. Dessa forma, podemos escrever e analisar os dois casos de $\text{interferência destrutiva em fase}$, além disso, atente à aproximação fornecida pelo enunciado:
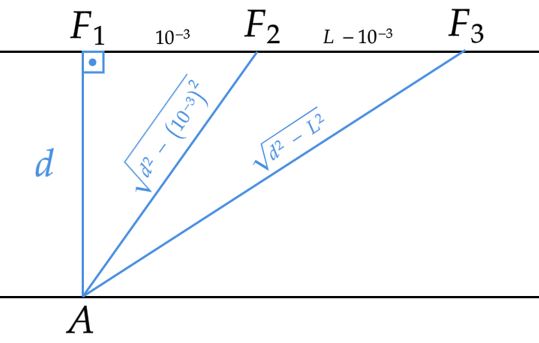 • Primeiro escurecimento
\begin{matrix} \Delta d_1 &=& \sqrt{d^2 + 10^{-6}} - d &=& d \cdot \bigg[ \bigg(1 + \dfrac{10^{-6}}{d^2}\bigg)^{1/2} - 1\bigg] &=& \dfrac{1}{2}\cdot \dfrac{10^{-6}}{d} &=& \dfrac{10^{-7}}{2} \ \pu{m}
\end{matrix}$\color{orangered}{Obs:}$ $\bigg(1 + \dfrac{10^{-6}}{d^2} \bigg)^{1/2} = \bigg(1 + \dfrac{1}{2} \cdot \dfrac{10^{-6}}{d^2} \bigg)$ e $d = 10,0 \ \pu{m}$
Assim,\begin{matrix} \Delta d_1 = N\cdot \dfrac{\lambda}{2} &,& \text{N = 1,3,5,7..} &,& \text{Para o primeiro: N = 1}
\end{matrix}Continuando,\begin{matrix} \fbox{$ {\dfrac{\lambda}{2} = \dfrac{10^{-7}}{2}}$} \ \ (1)
\end{matrix}
• Terceiro escurecimento
\begin{matrix} \Delta d_3 &=& \sqrt{d^2 + L^2} - d &=& d \cdot \bigg[ \bigg(1 + \dfrac{L^{2}}{d^2}\bigg)^{1/2} - 1 \bigg] &=& {\dfrac{1}{2} \cdot \dfrac{L^{2}}{d} } &=& {d\cdot \dfrac{L^{2}}{20} }
\end{matrix}Como é o terceiro escurecimento, $N = 5$, então:
\begin{matrix} \fbox{$ { \dfrac{5\lambda}{2} = {\dfrac{L^{2}}{20} } }$} \ \ (2)
\end{matrix}Por fim, dividindo $(2)$ por $(1)$:\begin{matrix} L = \sqrt{5} \cdot 10^{-3} \ \pu{m} &\Rightarrow& \fbox{$ L \approx 2,24 \ \pu{mm}$}
\end{matrix}\begin{matrix} Letra \ (E)
\end{matrix}
• Primeiro escurecimento
\begin{matrix} \Delta d_1 &=& \sqrt{d^2 + 10^{-6}} - d &=& d \cdot \bigg[ \bigg(1 + \dfrac{10^{-6}}{d^2}\bigg)^{1/2} - 1\bigg] &=& \dfrac{1}{2}\cdot \dfrac{10^{-6}}{d} &=& \dfrac{10^{-7}}{2} \ \pu{m}
\end{matrix}$\color{orangered}{Obs:}$ $\bigg(1 + \dfrac{10^{-6}}{d^2} \bigg)^{1/2} = \bigg(1 + \dfrac{1}{2} \cdot \dfrac{10^{-6}}{d^2} \bigg)$ e $d = 10,0 \ \pu{m}$
Assim,\begin{matrix} \Delta d_1 = N\cdot \dfrac{\lambda}{2} &,& \text{N = 1,3,5,7..} &,& \text{Para o primeiro: N = 1}
\end{matrix}Continuando,\begin{matrix} \fbox{$ {\dfrac{\lambda}{2} = \dfrac{10^{-7}}{2}}$} \ \ (1)
\end{matrix}
• Terceiro escurecimento
\begin{matrix} \Delta d_3 &=& \sqrt{d^2 + L^2} - d &=& d \cdot \bigg[ \bigg(1 + \dfrac{L^{2}}{d^2}\bigg)^{1/2} - 1 \bigg] &=& {\dfrac{1}{2} \cdot \dfrac{L^{2}}{d} } &=& {d\cdot \dfrac{L^{2}}{20} }
\end{matrix}Como é o terceiro escurecimento, $N = 5$, então:
\begin{matrix} \fbox{$ { \dfrac{5\lambda}{2} = {\dfrac{L^{2}}{20} } }$} \ \ (2)
\end{matrix}Por fim, dividindo $(2)$ por $(1)$:\begin{matrix} L = \sqrt{5} \cdot 10^{-3} \ \pu{m} &\Rightarrow& \fbox{$ L \approx 2,24 \ \pu{mm}$}
\end{matrix}\begin{matrix} Letra \ (E)
\end{matrix}

Ampliar Imagem

