Pensando na situação descrita no enunciado, podemos esboçar uma figura como abaixo: 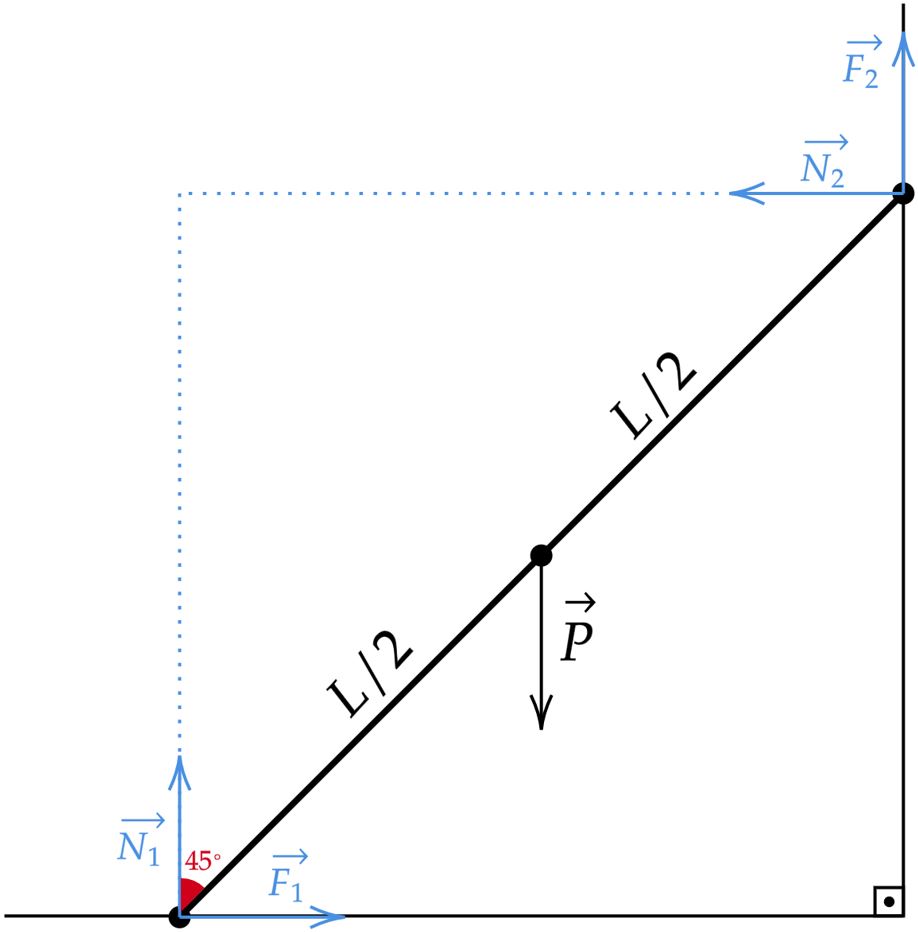Na iminência de deslizar, a força de atrito se encontra em estresse máximo, pensando no equilíbrio de forças, temos:\begin{matrix} \text{Equilíbrio forças:} & F_1 = N_2 &,& P = F_2 + N_1 \end{matrix}Com isso, pode-se escrever:\begin{matrix} N_1 \cdot \mu = N_2 &\Rightarrow& P = N_1 \cdot \mu^2 + N_1 &\therefore& \boxed{P = N_1 \cdot (1 + \mu^2)} & (1) \end{matrix}Analisando agora o momento das forças em relação ao ponto de contado da barra com a parede, têm-se:\begin{matrix} \Delta \tau = 0 &\Rightarrow& N_1 \cdot \bigg( \dfrac{\sqrt{2}}{2}L \bigg) = F_1 \cdot \bigg( \dfrac{\sqrt{2}}{2}L \bigg) + P \cdot \bigg( \dfrac{\sqrt{2}}{4}L \bigg) &\Rightarrow& 2N_1 = 2F_1 + P \end{matrix}Continuando,\begin{matrix} 2N_1 = 2N_1 \mu + N_1 \cdot (1 + \mu^2) &,& N_1 \ne 0 &\Rightarrow& \underbrace{\mu^2 +2 \mu -1 = 0}_{\Delta = 2\sqrt{2}} &\therefore& \mu = \sqrt{2} - 1 \end{matrix}Portanto, o coeficiente de atrito $\mu$ é: \begin{matrix} \mu = (2)^{1/2} - 1 & \tiny{\blacksquare} \end{matrix}\begin{matrix}Letra \ (B) \end{matrix}