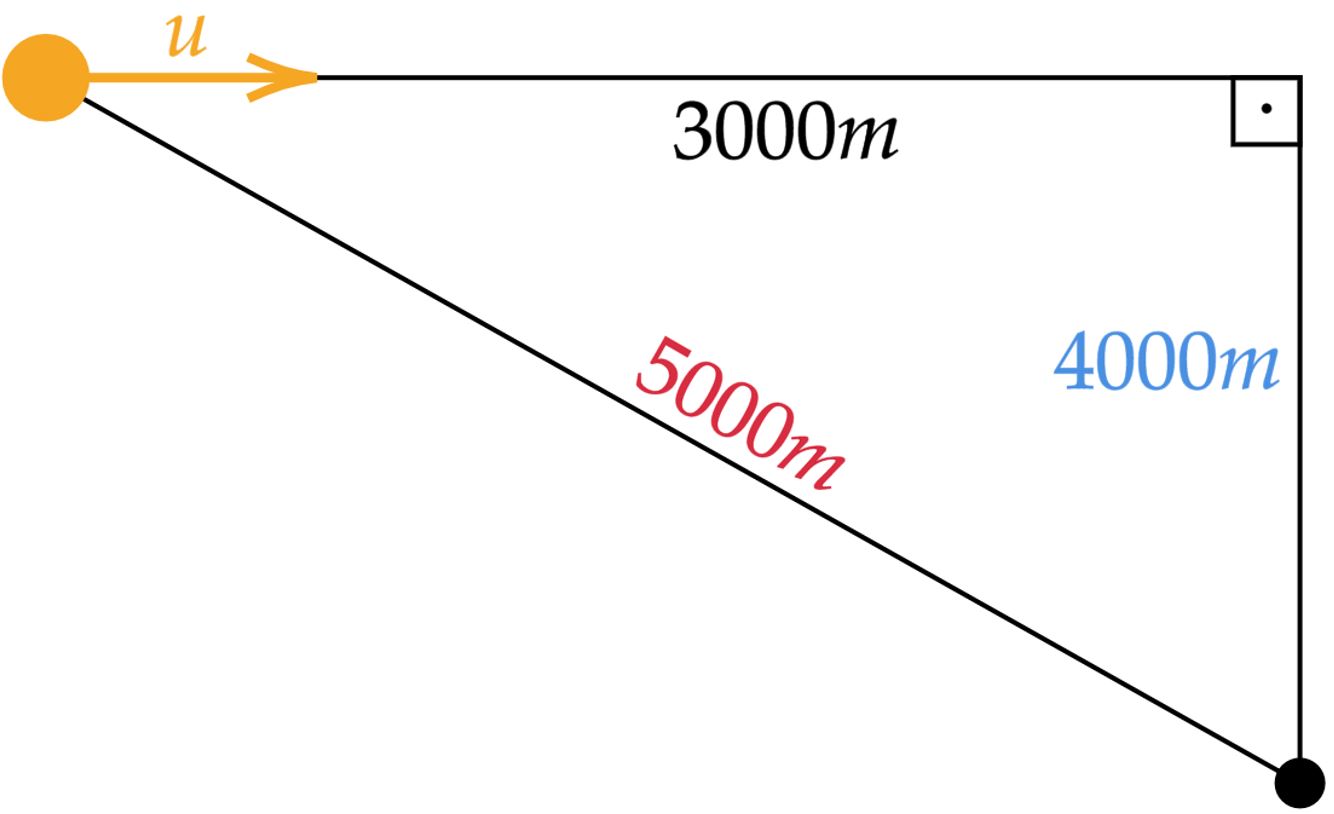
Esboçando a situação, não é difícil perceber que temos um triângulo retângulo pitagórico, com catetos valendo $3000 m$ e $4000 m $, consequentemente, a hipotenusa $5000 m$. Nessa perspectiva, entende-se que o intervalo de tempo do som sair de $A$ até o observador $(\Delta t)$ mais os quatro segundos de atraso até se emitir em $B$, deve ser igual ao tempo que o avião leva de $A$ até $B$ - $(\Delta t_1)$ - mais o tempo que o som leva de $B$ até o observador $(\Delta t_2)$, ou seja:\begin{matrix} \Delta t + 4 = \Delta t_1 + \Delta t_2 \end{matrix}Se o módulo da velocidade do avião for $u$, têm-se: \begin{matrix} {\Large{\frac{5000}{320}}} + 4 = {\Large{\frac{3000}{u}}} + {\Large{\frac{4000}{320}}} &\therefore& u \approx 421 \ m/s \end{matrix}\begin{matrix}Letra \ (D) \end{matrix}$• \ \text{Pensando de outra maneira:}$ Se ambos os sons - $A$ e $B$ - partissem ao mesmo tempo, qual seria a diferença de tempo para o observador?\begin{matrix} \Delta t - \Delta t_2 = {\Large{\frac{5000}{320}}} - {\Large{\frac{4000}{320}}} = {\Large{\frac{25}{8}}} s \end{matrix}Nesse viés, o som que parte de $A$ chegaria $25/8 s$ atrasado, contudo, na situação "real", o som de $A$ chega $4 s$ adiantado em relação a $B$. Com isso, entende-se que o adiantamento do som é devido ao tempo de percurso do avião até $B$, este tempo deve ser: \begin{matrix} \Delta t_1 = 4 + {\Large{\frac{25}{8}}} = {\Large{\frac{57}{8}}} s \end{matrix}Atente que, precisamos de $25/8 s$ para igualar o tempo de chegada de ambos os sons, os outros $4s$ serão responsáveis por adiantar o som que provém de $A$ em quatro segundos, logo:\begin{matrix} 3000 = u \Delta t_1 &\therefore& u \approx 421 \ m/s \end{matrix}