Um motociclista trafega numa estrada reta e nivelada atrás de um caminhão de de largura, perpendicularmente à carroceria. Ambos estão trafegando à velocidade constante de quando o caminhão se detém instantaneamente, devido a uma colisão. Se o tempo de reação do motociclista for , a que distância mínima ele deverá estar trafegando para evitar o choque apenas com mudança de trajetória?
Considere o coeficiente de atrito entre o pneumático e o solo $\mu = 0,80,$ aceleração gravitacional $g = 10,00\ m/s^{2}$ e que a trajetória original o levaria a colidir-se no meio da carroceria.
Pela situação descrita no enunciado, pode-se imaginar o evento abaixo:
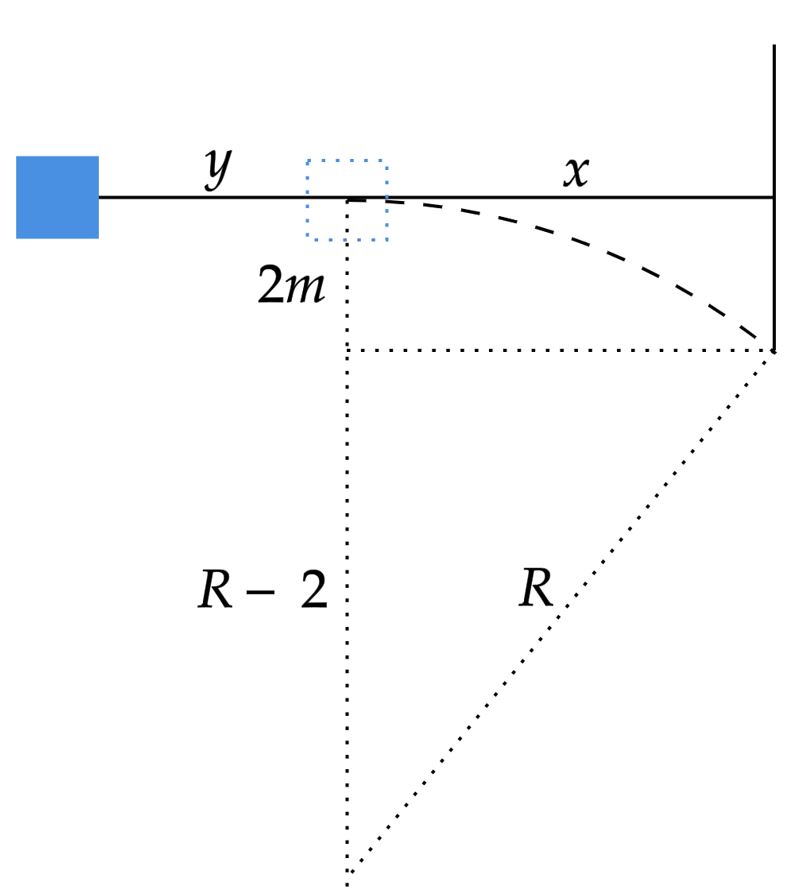Atente que, a distância mínima será aquela que o carro saia tangenciando a extremidade da carroceria do caminhão, conforme imagem acima. Nesse contexto, a distância $y$ é aquela que o carro percorre no intervalo de reação do motorista, então, como o movimento neste trajeto é retilíneo e uniforme, têm-se: \begin{matrix} v = 72 \ km/h = 20 \ m/s &\Rightarrow& y = v \cdot 0,5 &\therefore& y = 10,0 \ m
\end{matrix}Ao reagir, o motorista certamente irá esterçar o volante o máximo possível, nesse meio tempo, o carro irá realizar um arco de circunferência, neste movimento circular, pode-se escrever: \begin{matrix} R_{ct} = fat &\Rightarrow& {\Large{\frac{mv^2}{R}}} = \mu mg &\therefore& R = 50,0 \ m
\end{matrix}Relacionando a distância $x$ do caminhão por Pitágoras, temos: \begin{matrix} R^2 = (R-2)^2 + x^2 &\Rightarrow& x^2 = 50^2 - 48^2 &\therefore& x = 14, 0 \ m
\end{matrix}Portanto, a distância mínima que o carro deverá estar do caminhão é: \begin{matrix} x + y =24,0 \ m & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (D)
\end{matrix}
Ampliar Imagem
