Esboçando um gráfico arbitrário conforme enunciado : 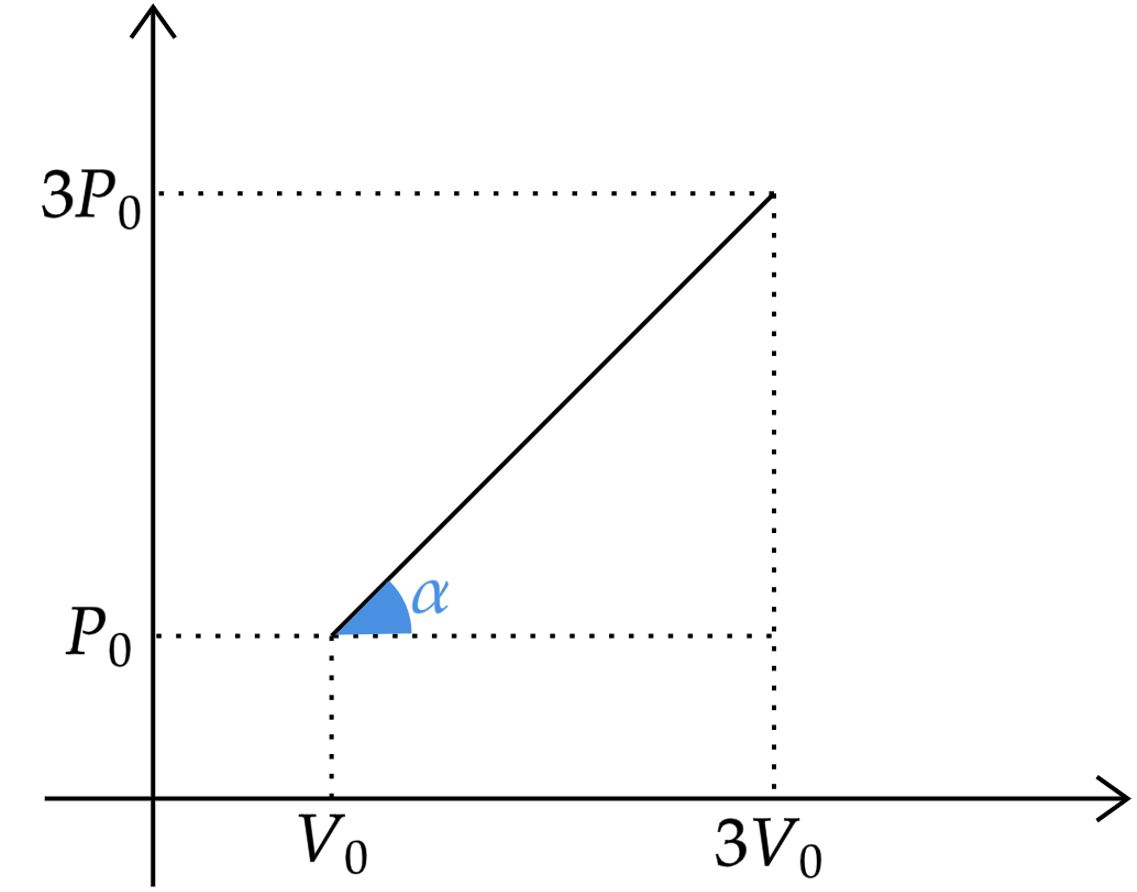Analisando o coeficiente angular, pode-se escrever:\begin{matrix} \tan{\alpha} = \dfrac{P}{V} = \dfrac{(3P_0 - P_0)}{(3V_0 - V_0)} = \dfrac{P_0}{V_0} \end{matrix}Nesse contexto, pela lei geral dos gases ideais, têm-se:\begin{matrix} P V = nRT &\Rightarrow&\tan{\alpha} \cdot V^2 = 2RT &\therefore& \boxed{T = \dfrac{P_0 V^2}{2R}} \end{matrix}Pensando agora no trabalho realizado, este é, basicamente, a área abaixo da reta do gráfico, área essa que representa um trapézio, logo:\begin{matrix}W = \dfrac{(P_0 + 3P_0)(3V_0 - V_0)}{2}= 4P_0V_0 & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (B) \end{matrix}

Perceba a priori que como o gráfico é uma reta e existe o pontos de associação $(V_{0} , P_{0})$ e $(3V_{0} , 3P_{0})$ , podemos afirmar que para um ponto qualquer $(V,P)$ , essa coordenada pode ser escrita da forma $(kV_{0} , kP_{0})$ , ou seja ,$V = kV_{0}$ e $P = kP_{0}$ , dessa forma podemos escrever que $kP_{0}V_{0} = (kP_{0}) \cdot V_{0} = (kV_{0}) \cdot P_{0} = \boxed{P \cdot V_{0} = V \cdot P_{0}} $ Pela equação de Clapeyron temos que $\dfrac{PV}{T} = nR \implies T = \dfrac{PV}{nR} = T = \dfrac{PV}{2R}$ Da primeira equação destacada podemos concluir que $P = \dfrac{V \cdot P_{0}}{V_{0}}$ $\therefore$ $T = \dfrac{PV}{2R} = \dfrac{\left(\dfrac{V \cdot P_{0}}{V_{0}}\right) V}{2R} = \boxed{T =\dfrac{P_{0}V^2}{2V_{0}R}}$ Para calcular o trabalho realizado pelo gás nesse processo basta calcular a área do trápezio formado abaixo do gráfico : $W = \dfrac{(P_{0} + 3P_{0}) \cdot (3V_{0} - V_{0})}{2} = \dfrac{4P_{0} \cdot 2V_{0}}{2} = \boxed{W = 4P_{0}V_{0}}$ $\textbf{Resposta : Alternativa B}$