A priori, sabe-se que é um tronco de pirâmide regular, logo, suas respectivas bases são regulares, ou seja, triângulos equiláteros. Nesse viés, observe a figura abaixo: 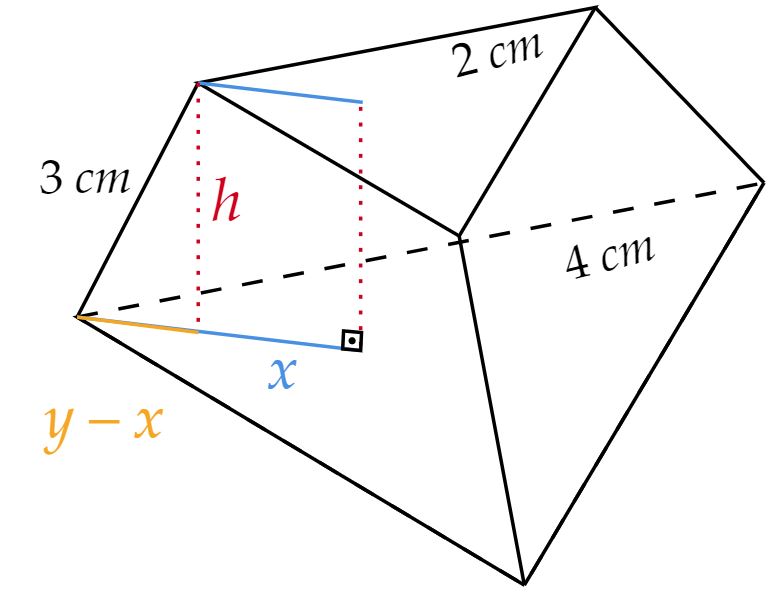Com isso, entende-se que o baricentro divide o triângulo numa razão $1:2$, assim, se a altura do triângulo for $t$, têm-se: \begin{matrix} t_1 = {{\dfrac{2\sqrt{3}}{2}}} &,& x = {{\dfrac{2}{3}}} \cdot t_1 &\therefore& x = {{\dfrac{2\sqrt{3}}{3}}} \\ \\ t_2 = {{\dfrac{4\sqrt{3}}{2}}} &,& y = {{\dfrac{2}{3}}} \cdot t_2 &\therefore& y = {{\dfrac{4\sqrt{3}}{3}}} \end{matrix}Por Pitágoras, constata-se: \begin{matrix} 3^2 = (y-x)^2 + h^2 &\Rightarrow& h = \sqrt{\dfrac{23}{3}}&\therefore& h = \sqrt{7,\overline{6}} \end{matrix} Portanto: \begin{matrix} \sqrt{7}< h < \sqrt{8} \\ \\ Letra \ (A) \end{matrix}