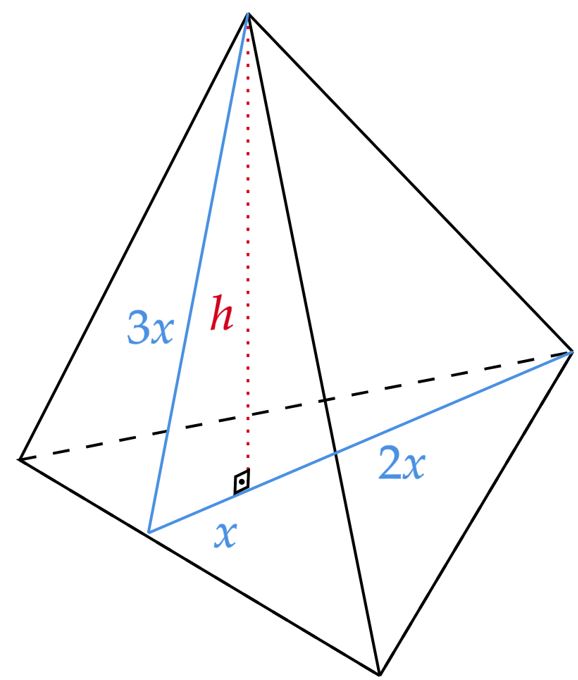
O tetraedro regular é um dos poliedros de Platão, este que apresenta quatro faces congruentes triangulares. Nessa perspectiva, denotemos a aresta do tetraedro de $L$, assim, a área total será: \begin{matrix} A_T = 4 \cdot {{ \left(\dfrac{L^2\sqrt{3}}{4}\right)}} = 6\sqrt{3} &\therefore& L =\sqrt{6} \ \pu{cm} \end{matrix}Analisando a base do tetraedro, precisamos encontrar o apótema da base $(x)$, faremos isso a partir do baricentro. Nesse viés, sabe-se que o triângulo da base assim como todos os outros são equiláteros, isto é, a mediana é igual a altura do triângulo, assim, se a altura do triângulo for $3x$, têm-se: \begin{matrix} 3x = {{\dfrac{L\sqrt{3}}{2} }}&\therefore& x = {{\dfrac{\sqrt{2}}{2} }} \end{matrix}Por fim, a altura $(h)$ do triângulo é encontrada aplicando Pitágoras, veja: \begin{matrix} (3x)^2 = x^2 + h^2 &\therefore& h = 2 \ \pu{cm} & \tiny{\blacksquare} \end{matrix} \begin{matrix} Letra \ (A) \end{matrix}