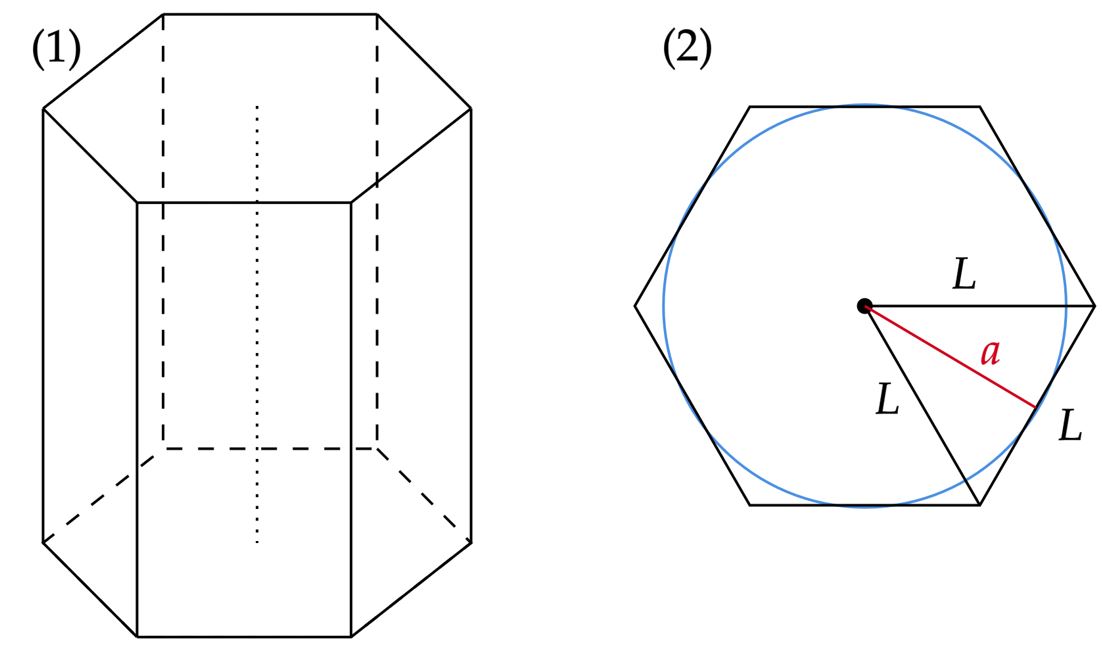
Da situação do enunciado, temos abaixo um prisma hexagonal regular $(1)$, e a visão frontal de sua base $(2)$, perceba que o apótema da base do hexágono $(a)$ é o raio do cone inscrito. Nesse viés, pela altura de um triângulo equilátero, pode-se encontrar o raio da base do cone, além disso, a área de um hexágono regular é: \begin{matrix} a = {{\dfrac{L\sqrt{3}}{2}}} &,& A_{hexágono} = 6 \cdot {{ \left(\dfrac{L^2\sqrt{3}}{4} \right)}} \end{matrix}Então o volume do prisma e do cone são: \begin{matrix} V_{prima} = A_{hexágono} \cdot (2L) &,& V_{cone} =\pi \ a^2 \cdot (2L) \end{matrix}Portanto, a razão solicitada:\begin{matrix} {{\dfrac{V_{prima}}{V_{cone}} }} = {{\dfrac{A_{hexágono}}{\pi a^2} } } &\therefore& {{\dfrac{V_{prima}}{V_{cone}} }} = {{\dfrac{(6\sqrt{3})}{\pi}}} & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (D) \end{matrix}