A priori, temos as situações abaixo: 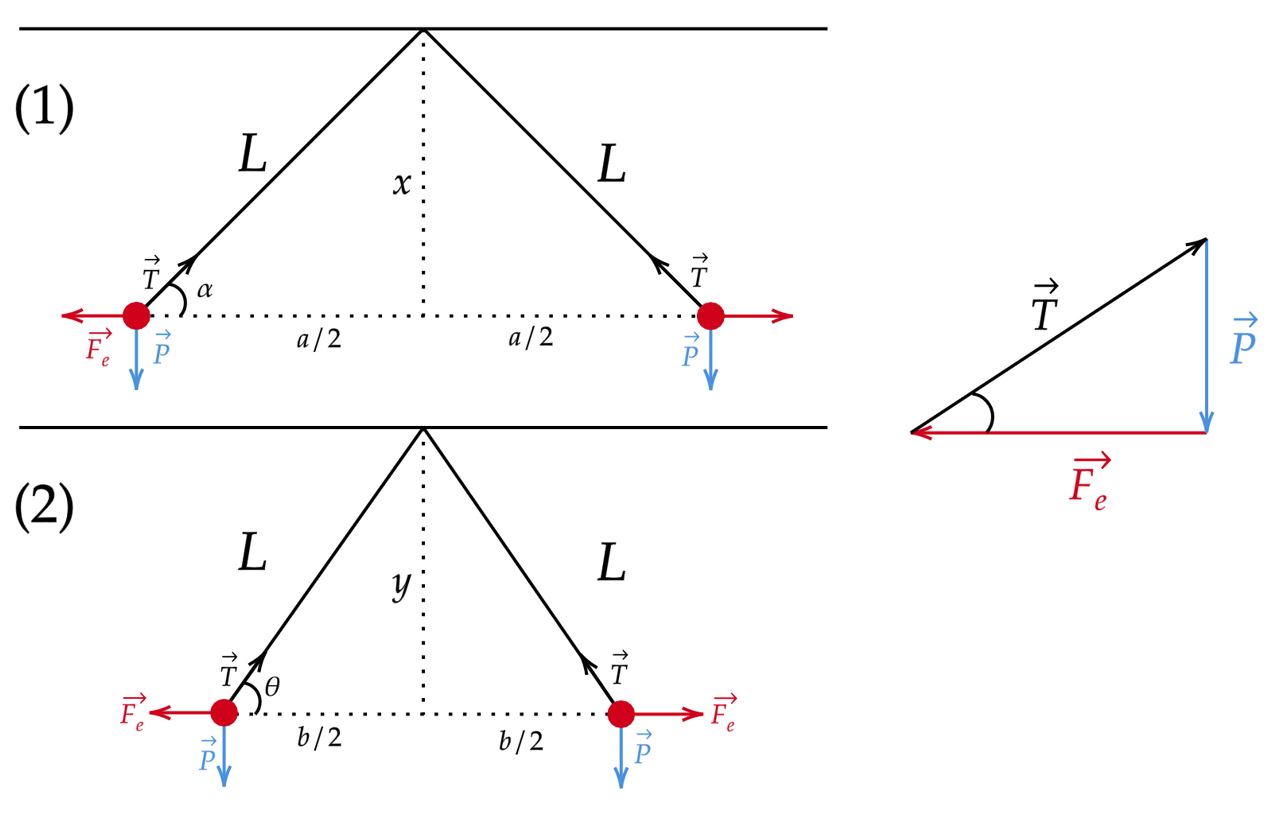Veja que, como o sistema está em equilíbrio, têm-se a soma vetorial acima, a qual podemos escrever: \begin{matrix} \tan{\alpha} = \large{\frac{P}{F_1} } &,& \tan{\theta} = \large{\frac{P}{F_2} } &\Rightarrow& \large{\frac{\tan{\alpha}}{\tan{\theta}} = \frac{F_2}{F_1}} \end{matrix} Por outro lado, da geometria do problema, \begin{matrix} \tan{\alpha} = \large{\frac{2x}{a} } &,& \tan{\theta} = \large{\frac{2y}{b} } &\Rightarrow& \fbox{$ \large{\frac{xb}{ya} = \frac{F_2}{F_1}} $}& (I)\end{matrix}Atente que, no instante posterior ao contato, as cargas serão $q_2 = q_1/2$ , visto que as esferas são idênticas. Portanto, de $(I)$ temos: \begin{matrix} \Large{\frac{xb}{ya}} &=& \Large{\frac{\frac{K(q_2)^2}{b^2}}{\frac{K(q_1)^2}{a^2}}} &\Rightarrow& \fbox{$4b^3.x = a^3 .y$} & (II) \end{matrix}Agora, da trigonometria do problema, por$\text{ Pitágoras}$, temos: \begin{matrix} x = \sqrt{L^2 -(a/2)^2} &,& y= \sqrt{L^2 -(b/2)^2} \end{matrix}Substituindo os resultados acima em $(II)$, não é difícil encontrar: \begin{matrix} \fbox{$b= a/4^{1/3}$} \\ \\ Letra \ (E) \end{matrix}