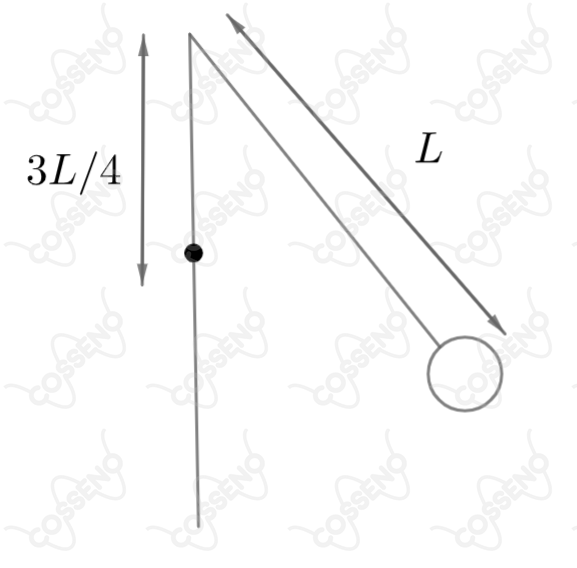
Um pêndulo simples oscila com um período de . Se cravarmos um pino a uma distância do ponto de suspensão e na vertical que passa por aquele ponto, como mostrado na figura, qual será o novo período do pêndulo? Desprezar os atritos. Considere ângulos pequenos tanto antes quanto depois de atingir o pino.
CossenoGPT
Teste
gratuitamente agora
mesmo! 
Analisando a situação, pode-se pensar em dois pêndulos, o inicial de comprimento $L$, e outro menor de comprimento $L/4$. Além disso, observe que cada um será responsável por metade do movimento, ou seja, o período total é a soma da metade dos períodos de cada um. Nesse viés, pode-se pensar na situação abaixo:
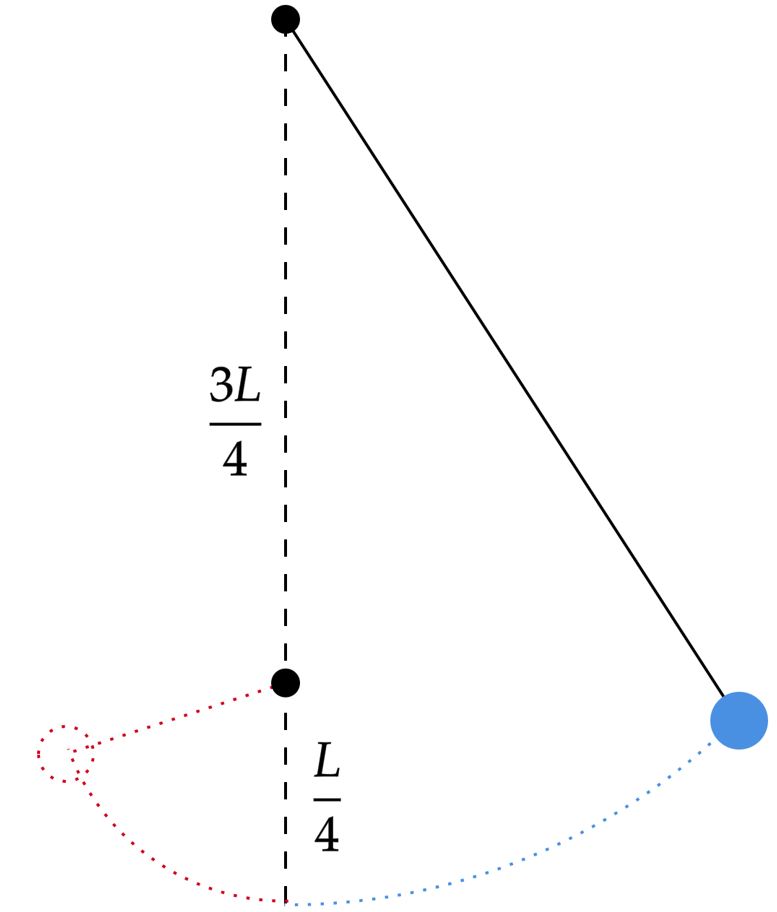Conhecido o período de um pêndulo simples, temos: \begin{matrix}\begin{cases}
\text{Pêndulo (L):} & 2 = {2\pi }{\sqrt{\dfrac{L}{g}}} \\
\text{Pêndulo (L/4):} & T = {2\pi }{\sqrt{\dfrac{L}{4g}}}
\end{cases} &\therefore& T = 1 \ \pu{s}&\end{matrix}Com isso, o período ${(P)}$ deste novo pêndulo é: \begin{matrix} P = 1 + \dfrac{T}{2} &\therefore& P =1,5 \ \pu{s} & \tiny{\blacksquare}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}
Ampliar Imagem
