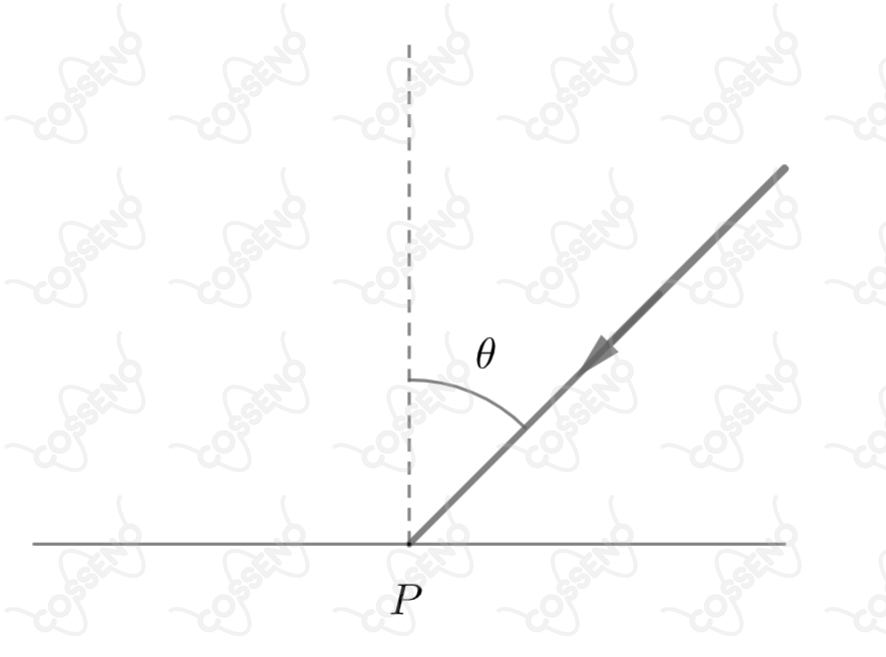
Um raio luminoso incide com um ângulo $\theta$ em relação à normal, sobre um espelho refletor. Se esse espelho girar de um ângulo igual a $\theta $ em torno de um eixo que passa pelo ponto $P$ e é perpendicular ao plano da figura, qual o ângulo de rotação do raio refletido?
A dificuldade da questão é mais da construção do problema, por isso, observe o esboço abaixo para quando o giro é anti-horário. Agora, perceba que o ângulo de rotação do raio refletido foi denotado por $\varphi$, enquanto os ângulos de incidência e reflexão foram chamados de $\alpha$, dessa forma, podemos solucionar a situação com duas equações, veja:
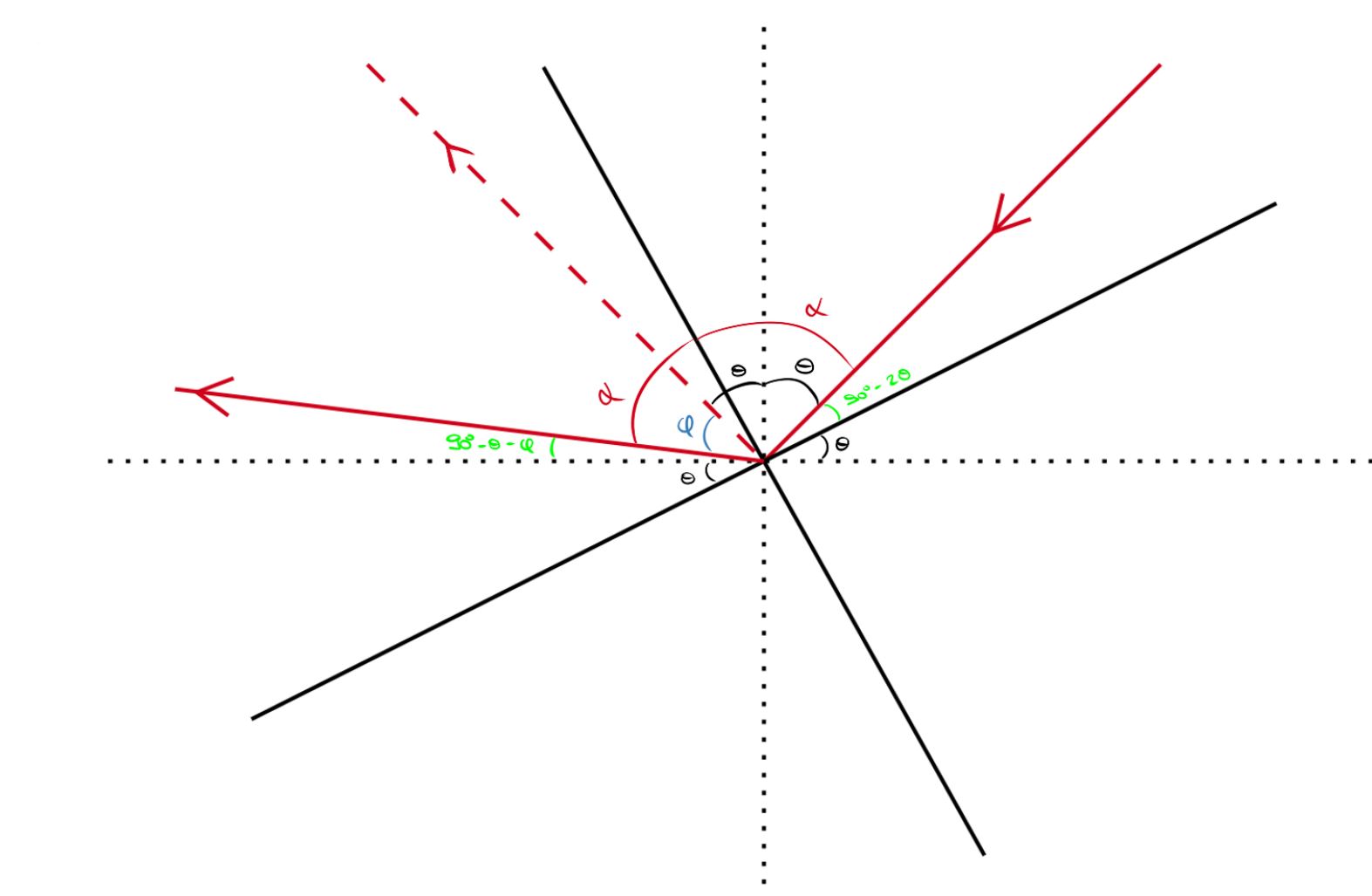\begin{matrix} \alpha + (90^{\circ} - 2\theta) = 90^{\circ} &\Rightarrow& \fbox{$\alpha = 2\theta$}
\end{matrix}
Além disso,
\begin{matrix} \alpha + (90^{\circ} - \theta - \varphi) + \theta = 90^{\circ} &\Rightarrow& \fbox{$\varphi= 2\theta$}
\end{matrix}Atente que, se a rotação fosse horária, o raio estaria incidindo perpendicularmente à superfície do espelho, isto é, não haveria ângulo de reflexão, fazendo com que a variação fosse a mesma da anterior, quer dizer, $2\theta$. \begin{matrix} Letra \ (D)
\end{matrix}
Ampliar Imagem
