Podemos representar as situações de frequências fundamentais por: 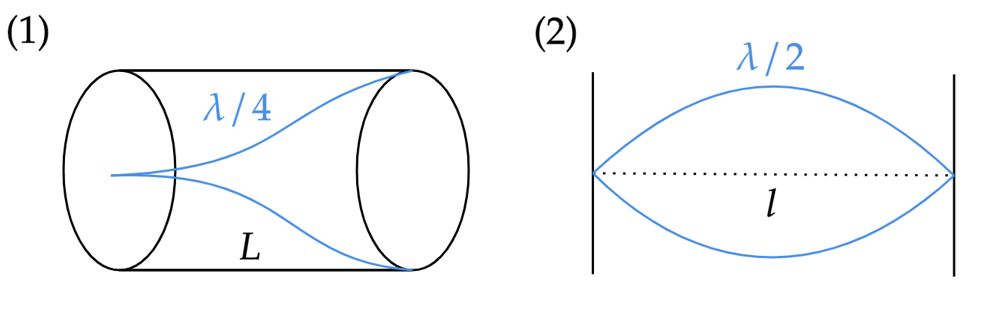Do caso $(1)$, iremos determinar a frequência como:\begin{matrix} L = \dfrac{\lambda}{4} &\Rightarrow& \lambda = 4 \ m &,& v_s = \lambda.f &\Rightarrow& \fbox{$f = 85 Hz$} \end{matrix}$v_s:$ velocidade do som Já no caso $(2)$, encontraremos a massa da corda a partir da $\text{Equação de Taylor}$:\begin{matrix} l = \dfrac{\lambda}{2} &\Rightarrow& \lambda = 2 \ m &,& v = {\sqrt{\dfrac{T}{\mu}}} &,& \mu = {\dfrac{m}{l}} &\Rightarrow& \lambda f= {\sqrt{\dfrac{10}{m}}} \end{matrix}\begin{matrix} \fbox{$m \cong 3,5 \cdot 10^{-4} \ kg$} \\ \\ Letra \ (D) \end{matrix}