Um recipiente, cujas secções retas dos êmbolos valem e , está cheio de um líquido de densidade , como mostra a figura. Os êmbolos estão unidos entre si por um arame fino de comprimento . Os extremos do recipiente estão abertos. Despreze o peso dos êmbolos, do arame e quaisquer atritos. Quanto vale a tensão no arame
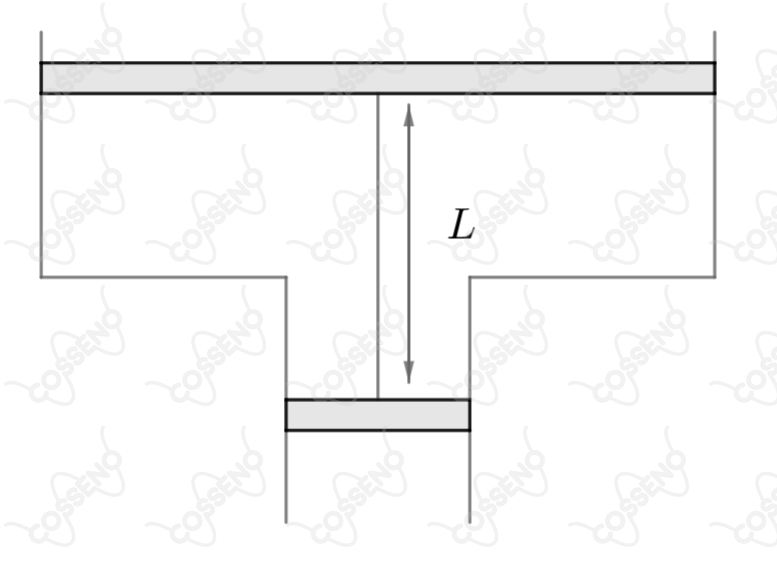
$S_1:$ área da tampa superior.
$S_2:$ área da tampa inferior.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

O êmbolo de secção $S_{1}$ é puxado para baixo pela força de tensão $T$ do arame e empurrado para baixo pela força atmosférica $F_{atm}$ , como o fluído é incompressível , então existe uma força $F_{1}$ para cima atuante sobre o êmbolo de secção $S_{1}$ , tal que $F_{1} = T + F_{atm}.$
O êmbolo de secção $S_{2}$ é puxado para cima pela força de tensão $T$ do arame e empurrado para cima pela força atmosférica $F_{atm}$ , pelo fato do fluído ser incompressível(caso ideal) , então existe uma força $F_{2}$ para baixo atuante sobre o êmbolo de secção $S_{2}$ , tal que $F_{2} = T + F_{atm}.$
Dessas duas informações podemos escrever que :
$F_{1} = T + F_{atm} = P_{1} \cdot S_{1}= T +P_{atm} \cdot S_{1} \implies \dfrac{T}{S_{1}} = P_{1} - P_{atm}$
$F_{2} = T + F_{atm} = P_{2} \cdot S_{2}= T +P_{atm} \cdot S_{2} \implies \dfrac{T}{S_{2}} = P_{2} - P_{atm}$
$\therefore$
$ \dfrac{T}{S_{2}} -\dfrac{T}{S_{1}}= P_{2} - P_{atm} - (P_{1} - P_{atm} )$
$T\left(\dfrac{1}{S_{2}} - \dfrac{1}{S_{1}}\right) = P_{2} - P_{1}$
Note que $P_{2} - P_{1}$ é a diferença de pressão entre os pontos de aplicação da força $F_{2}$ e $F_{1}$ , essa diferença é dada por $P_{2} - P_{1} = \rho g L$.
$\therefore$
$T\left(\dfrac{1}{S_{2}} - \dfrac{1}{S_{1}}\right) =\rho g L = T\left(\dfrac{S_{1} - S_{2}}{S_{1}S_{2}}\right) $
$\implies \boxed{T = \dfrac{\rho gLS_{1}S_{2}}{(S_{1} - S_{2})}}$
$\textbf{Resposta : Alternativa A}$
Tomemos $P_1$ e $P_2$, respectivamente, como as pressões exercidas pelo líquido nas secções de áreas $S_1$ e $S_2$ . Seja também $P_A$ a pressão atmosférica. Equilibrando as forças na tampa superior, temos:$$(1)~~\color{green}{P_1 S_1 = P_A S_1 + T}$$Pela Lei de Stevin, sabe-se que: $P_2 = P_1 + \rho g L$, em que $\rho g L$ é a pressão da coluna de altura $L$ do líquido.
Equilibrando agora na tampa inferior, temos:$$P_2 S_2 = P_A S_2 + T \implies (2)~~\color{green}{P_1S_2 + \rho g L S_2 = P_A S_2 + T}$$
Multiplicando agora a relação $(1)$ por $S_2$, bem como a relação $(2)$ por $S_1$, encontra-se:$$\begin{cases} P_1 S_1 S_2 = P_A S_1 S_2 + T S_2 ~~(3)\\
P_1S_1S_2 + \rho g L S_1S_2 = P_A S_1S_2 + TS_1 ~~(4)\end{cases}$$Calculando $(4)$ - $(3)$ , temos:$$\rho g L S_1S_2 = T(S_1-S_2) \implies \boxed{T = \rho g L S_1S_2/(S_1-S_2)}$$
$$\text{Alternativa } \mathbb{(A)}$$


