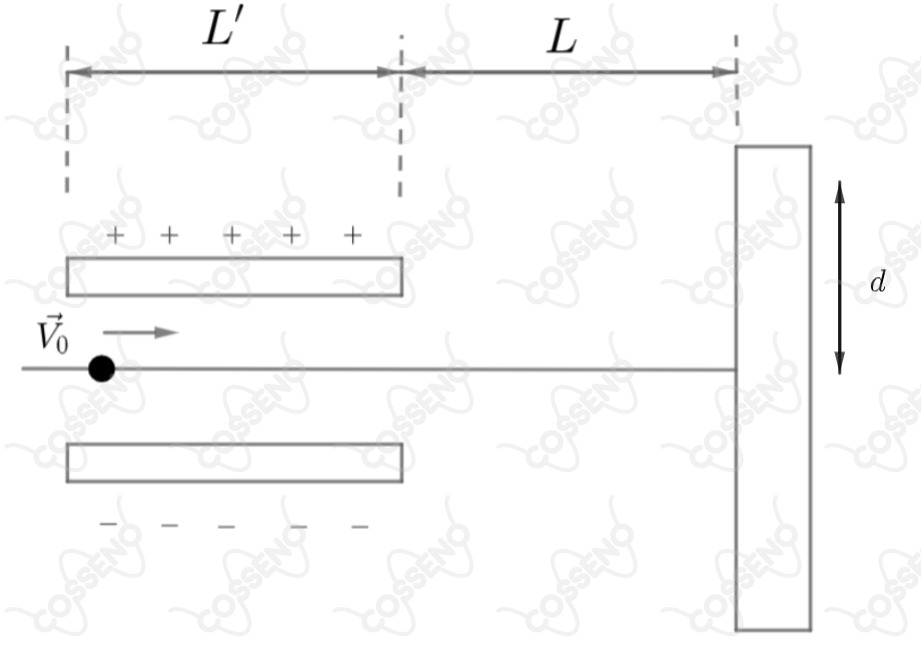
Duas placas planas e paralelas, de comprimento , estão carregadas e servem como controladoras em um tubo de raios catódicos. A distância das placas até a tela do tubo é . Um feixe de elétrons de massa penetra entre as placas com uma velocidade , como mostra a figura. Qual é o campo elétrico entre as placas se o deslocamento do feixe na tela é igual a ?
A priori, a questão não deixa exatamente explícito, mas deve-se considerar o meio como o vácuo. Principalmente, pois quando o enunciado fala $\text{tubo de raios catódicos}$, nos remete aos $\text{Tubos de Crookes}$.
Agora, perceba que a velocidade horizontal em todo o movimento é constante e, igual a $V_0$, assim, durante o movimento dentro da placa, temos:
\begin{matrix} t = \dfrac{L^′}{V_0}
\end{matrix}A força resultante no elétron será a força elétrica:
\begin{matrix}|F_r|=|F_e| &\Rightarrow & m.a = E.e &\Rightarrow & a = \dfrac{E.e}{m}
\end{matrix}
Podemos ainda dizer que, a velocidade vertical do elétron ao chegar no final da placa é:
\begin{matrix} v_y = 0 + a.t &\Rightarrow & v_y = \dfrac{E.e}{m} \cdot \dfrac{L^′}{V_0}
\end{matrix}
A variação de altura que o elétron sofre até o final da placa:
\begin{matrix} v_y^2 = 0^2 + 2.a.\Delta h &\Rightarrow & \Delta h = \dfrac{(L^′)^2.E.e}{2m.V_0}
\end{matrix}
Após sair do campo das placas, a velocidade é constante, assim, podemos escrever:
\begin{matrix} T &= &\dfrac{L}{V_0}&= & \dfrac{d - \Delta h}{V_y}
\end{matrix}
Ajeitando e substituindo os valores na igualdade, chegaremos em algo como:
\begin{matrix} E = \dfrac{m\cdot V_0^2 \cdot d}{e \cdot L^′(L + \dfrac{L^′}{2})} \\ \\ Letra \ (C)
\end{matrix}
