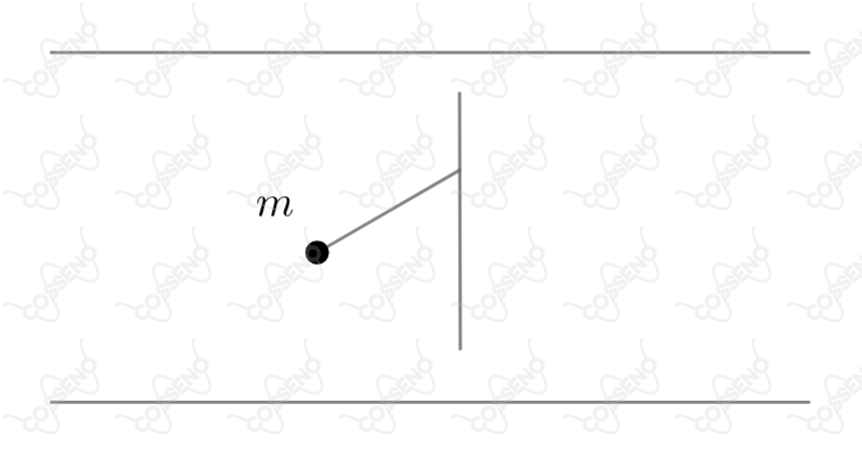
Uma pequena esfera metálica, de massa , está suspensa por um fio fino de massa desprezível, entre as placas de um grande capacitor plano, como mostra a figura. Na ausência de qualquer carga tanto no capacitor quanto na esfera o período de oscilação da esfera é . Logo em seguida uma carga é colocada sobre a esfera e a placa superior do capacitor é carregada positivamente. Nessas novas condições o período de oscilação da esfera torna-se . Qual é a força que o campo elétrico do capacitor exerce sobre a esfera?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, perceba que o primeiro período é o dobro do segundo, assim, temos: \begin{matrix} (1)& T_1 &=& 2T_2
\end{matrix}Com conhecimento da equação do período de um pêndulo simples, temos para o primeiro caso:
\begin{matrix} T_1 &=& 2\pi\Large{ \sqrt{ \frac{l}{g} }}
\end{matrix}Agora, sabido que a carga e a placa superior são positivas, teremos um campo elétrico na mesma direção e sentido da gravidade. Nesse contexto, como a carga é positiva, atuará uma força elétrica de mesma direção e sentido da força peso. Em suma, devemos encontrar a gravidade aparente $(g_p)$ no local:
\begin{matrix} m.g_p = P + F_e &\Rightarrow& g_p = g + \large{\frac{e.E}{m}}
\end{matrix} Novamente, da equação do período, \begin{matrix} T_2 &=& 2\pi\Large{ \sqrt{ \frac{l}{g + \large{\frac{e.E}{m}}} }}
\end{matrix}
De $(1)$, têm-se:
\begin{matrix} 2\pi\Large{ \sqrt{ \frac{l}{g} }} &=&4\pi\Large{ \sqrt{ \frac{l}{g + \large{\frac{e.E}{m}}} }} &\Rightarrow& mg + eE = 4mg
\end{matrix} Portanto, \begin{matrix} F_e = 3mg \\ \\ Letra \ (A)
\end{matrix}

