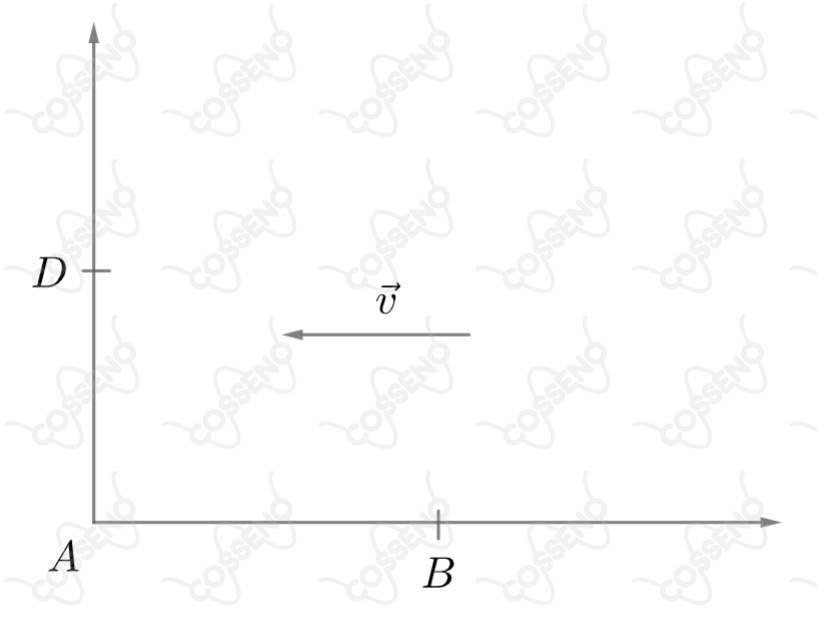
Uma ventania extremamente forte está soprando com uma velocidade na direção da seta mostrada na figura. Dois aviões saem simultaneamente do ponto e ambos voarão com uma velocidade constante em relação ao ar. O primeiro avião voa contra o vento até o ponto e retorna logo em seguida ao ponto , demorando para efetuar o percurso total um tempo . O outro voa perpendicularmente ao vento até o ponto e retorna ao ponto , num tempo total . As distâncias e são iguais a . Qual é a razão entre os tempos de voo dos dois aviões?
CossenoGPT
Teste gratuitamente agora mesmo! 

Começando pelo primeiro avião, vejamos:
• Na ida: \begin{matrix} \huge{\color{royalblue}{\longrightarrow} \color{orangered}{\leftarrow}} &\Rightarrow& V_1 = c - v
\end{matrix}• Na volta:
\begin{matrix} \huge{\color{royalblue}{\longleftarrow} \color{orangered}{\leftarrow}} &\Rightarrow& v_1 = c + v
\end{matrix}Logo, o tempo total será: \begin{matrix} t_1 = {\large{\frac{L}{c-v}}} + {\large{\frac{L}{c+v}}} &\therefore& t_1 = {\large{\frac{2.L.c}{c^2 - v^2}}} &,& \color{royalblue}{•} \vec{c} & \color{orangered}{•} \vec{v}
\end{matrix}Já para o segundo avião:
• Na ida: \begin{matrix} \huge{\color{yellowgreen}{\uparrow}_{\color{royalblue}{\nearrow}}^{\color{orangered}{\longleftarrow}}} &\Rightarrow& c^2 = V_2^2 + v^2 &\therefore& V_2 = \sqrt{c^2 - v^2}
\end{matrix}• Na volta: \begin{matrix} \huge{\color{yellowgreen}{\downarrow}_{{\color{orangered}{\longleftarrow}}}^{\color{royalblue}{\searrow} }} &\Rightarrow& c^2 = v_2^2 + v^2 &\therefore& v_2 = \sqrt{c^2 - v^2}
&,& \color{royalblue}{•} \vec{c} & \color{orangered}{•} \vec{v} & \color{yellowgreen}{•} \vec{V}_2,\vec{v}_2
\end{matrix}Logo, o tempo total será: \begin{matrix} t_2 = {\large{\frac{L}{\sqrt{c^2 - v^2}}}}
+ {\large{\frac{L}{\sqrt{c^2 - v^2}}}}
\end{matrix}Por fim: \begin{matrix} {\large{\frac{t_2}{t_1}}} = {\Large{\frac{\frac{2.L}{\sqrt{c^2 - v^2}}}{\frac{2.L.c}{c^2 - v^2} }}} &\Rightarrow&
{\large{\frac{t_2}{t_1} }}= {\large{\frac{c^2 - v^2}{c.\sqrt{c^2 - v^2}}}} = {\large{\frac{\sqrt{c^2 - v^2}}{c}}} &\therefore& {\large{\frac{t_2}{t_1}}} = \sqrt{1 - {\large{\frac{v^2}{c^2}}}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

