Segundo enunciado, a pirâmide apresenta base quadrada, logo, a aresta da base vale $8 \ m$. Nesse viés, pela altura da pirâmide e o apótema da base, aplicando Pitágoras, encontra-se a altura dos triângulos que compõem a lateral da pirâmide, veja: 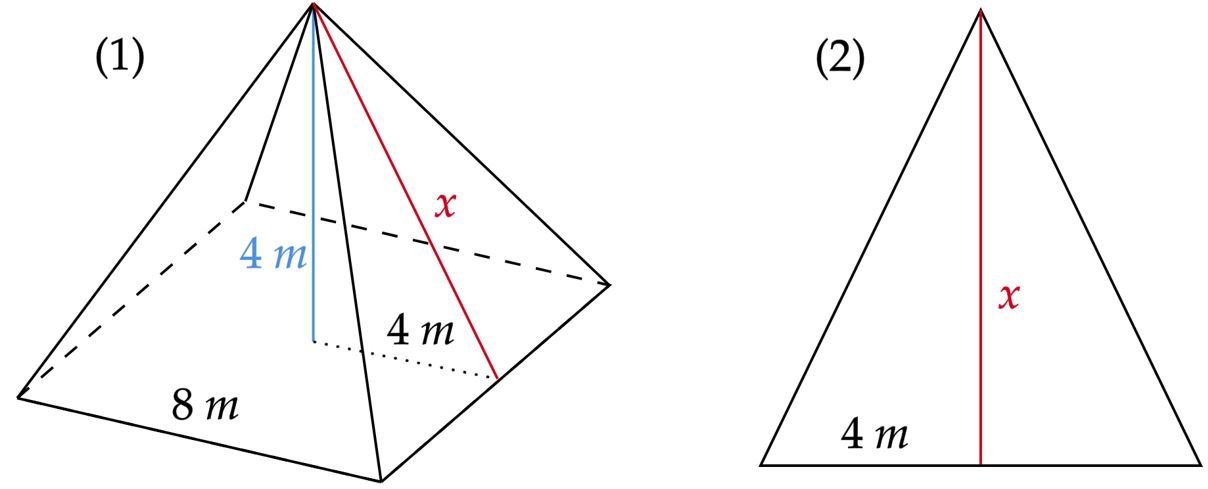Altura $x$: \begin{matrix} x^2 = 4^2 + 4^2 &\therefore& x = 4\sqrt{2} \ \pu{m} \end{matrix}A área de um dos lados: \begin{matrix} A = 2 \cdot \left( \dfrac{4 \cdot 4\sqrt{2} }{ 2} \right) &\therefore& A =16 \sqrt{2} \ \pu{m^2} \end{matrix}Como são quatro lados, a área lateral: \begin{matrix} A_{Lateral} = 4 \cdot A &\therefore& A_{Lateral} = 64 \sqrt{2} \ \pu{m^2} & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (B) \end{matrix}