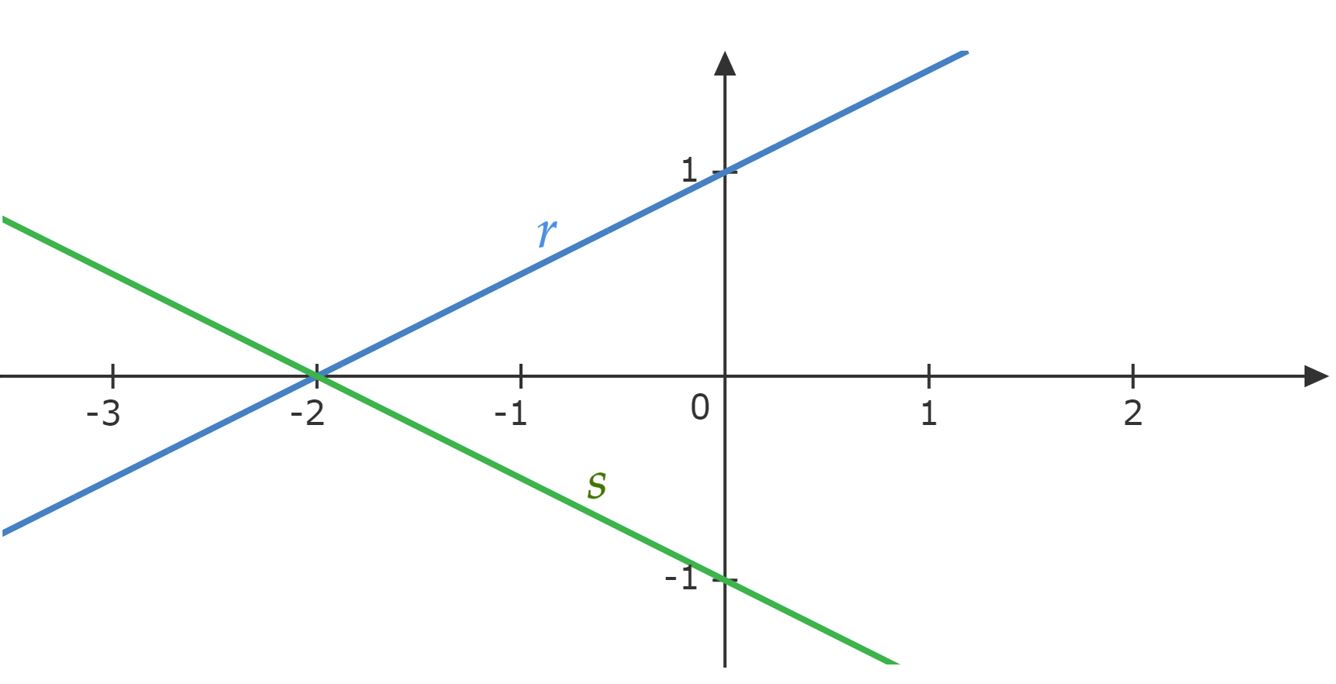
O problema em si não é difícil se você tentar esboçar a situação, veja que a equação da reta $(r)$ intercepta os eixos nos pontos $(-2,0)$ e $(0,1)$, logo, a reta $(s)$ deve passar por $(-2,0)$, pois ela é simétrica ao eixo das abscissas. Nessa perspectiva, a reta $(s)$ precisa passar num ponto simetricamente oposto ao $(0,1)$, este que está sobre o eixo das coordenadas, assim, $(s)$ deve passar em $(0,-1)$. Portanto, com esses dois pontos podemos escrever a equação segmentária da reta $(s)$:\begin{matrix} \dfrac{x}{-2} +\dfrac{y}{-1} = 1 &\therefore& \fbox{$x +2y+2 - 0$} \end{matrix} \begin{matrix} Letra \ (D) \end{matrix}