Uma das circunferências que passa pelo ponto e tangencia as retas e tem sua equação dada por:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Segundo o enunciado, as duas retas tangenciam a(s) circunferência(s), isto é, a distância entre o(s) centro(s) e a(s) reta(s) é (são) semelhante(s), no caso, iguais ao(s) raio(s). Dessa forma, denotemos o centro de $C: (q \ , \ w)$, continuando:\begin{matrix} {d = \dfrac{|a.x +b.y + c|}{\sqrt{a^2 + b^2}} }
\end{matrix}Assim, dadas as retas: \begin{matrix}R = {{\dfrac{|1.q +1.w - 2|}{\sqrt{1^2 + 1^2}}}} = {\large{\frac{|1.q - 1.w |}{\sqrt{1^2 + (-1)^2}} }} \\ \\ |q + w - 2| = |q - w| \\ \\ q^2 + w^2 + 4 + 2.(q.w - 2q - 2w) = q^2 + w^2 - 2qw \\ \\ q + w - qw - 1 = 0 \\ \\ \fbox{$ (1-q).(w -1) = 0 \\ (q-1).(1 -w) = 0$}
\end{matrix}Não é difícil encontrar as soluções dessa equação,\begin{matrix} q = 1 & , & w = 1 & \Rightarrow & \text{Não satisfaz, pois o raio seria nulo} \\ \\
q = -1 & , & w = 1 & \Rightarrow& \text{Satisfaz} \\ \\
q = 1 & ,& w = -1 & \Rightarrow & \text{Satisfaz}
\end{matrix}Substituindo qualquer um dos dois resultados na nossa primeira equação, pode-se encontrar o raio: \begin{matrix}R = {\large {\frac{2}{\sqrt{2}} }}= \sqrt{2}
\end{matrix}Escrevendo as equações das nossas duas possíveis circunferências: \begin{matrix} (q - 1)^2 &+& (w +1)^2 &=& 2 & \Rightarrow & \text{Há gabarito} \\ \\ (q + 1)^2 &+& (w - 1)^2 &=& 2 & \Rightarrow & \text{Não há gabarito}
\end{matrix}\begin{matrix} Letra \ (B)
\end{matrix}$\color{orangered}{Obs:}$ Você poderia abordar a questão de formas diferentes, por exemplo, veja que as retas são perpendiculares $(m_{r_1} . m_{r_2}= -1)$, assim, há vários modos de cair na mesma equação: $q + w - qw - 1 = 0$
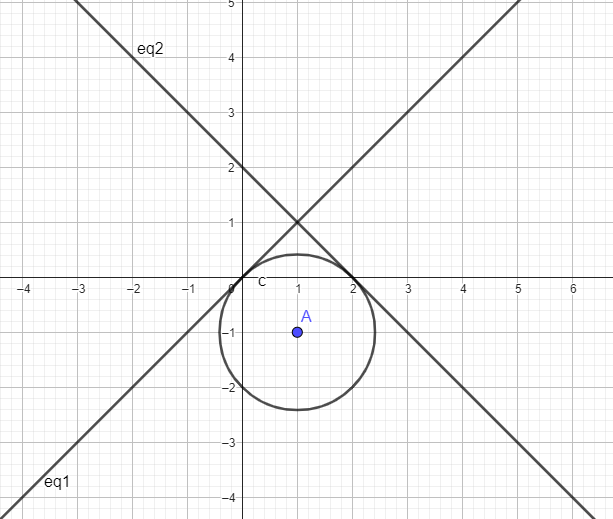
Ao esboçar um gráfico das 2 retas, observamos que a circunferência pode estar localizada em 2 lugares possíveis, já que deve passar por (0,0) e ser tangente às duas retas. Como a reta y = x passa por (0,0), pode se concluir que (0,0) é um ponto de tangência entre essa reta e a circunferência. Ou seja, ao substituir x = y na equação da circunferência, a equação deve ser zerada. Chegando, dessa forma, à alternativa B. É lógico que, em uma prova discursiva, essa tentativa não caiba.

Ampliar Imagem


