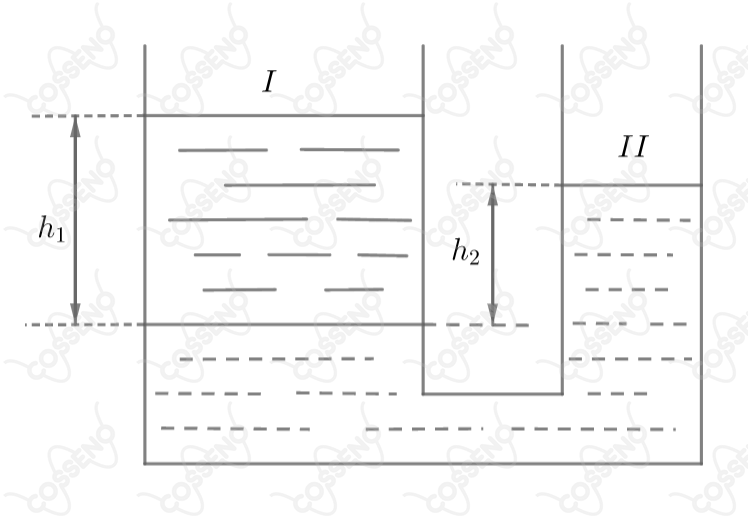
Dois vasos comunicantes contêm dois líquidos não miscíveis, I e II, de massas específicas e , sendo , como mostra a figura. Qual é a razão entre as alturas das superfícies livres desses dois líquidos, contadas a partir da sua superfície de separação?
Sabido que, num líquido em equilíbrio, todos os pontos pertencentes ao mesmo nível horizontal formam uma região isobárica (mesma pressão). Dada a linha de nível da imagem, podemos escrever:
\begin{matrix} P_1 = P_2
\end{matrix}
Em que $P_1$ é a pressão no ponto de separação dos líquidos (vaso da esquerda), e $P_2$ é a pressão situada no vaso da direita, na mesma linha horizontal.
Pelo Teorema de Stevin, podemos escrever:\begin{matrix} P_1 - P_{atm} = d_1.g.h_1 &,& P_2 - P_{atm} = d_2.g.h_2 &\Rightarrow& d_1.g.h_1 = d_2.g.h_2
&\therefore&
{\fbox{$\dfrac{h_1}{h_2} = \dfrac{d_2}{d_1} $}}
\end{matrix}\begin{matrix}Letra \ (C)
\end{matrix}
