Na figura abaixo, a massa esférica pende de um fio de comprimento , mas está solicitada para a esquerda por uma força que mantém a massa apoiada contra uma parede vertical , sem atrito. Determine os valores de e de (reação da parede), respectivamente.
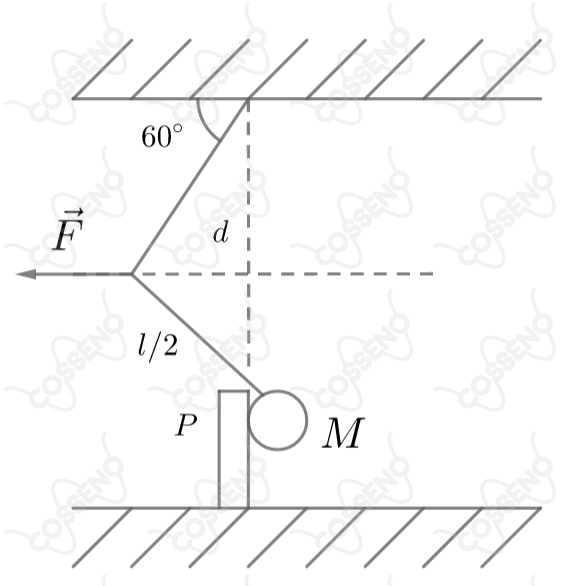
O raio da esfera $<$$<$$L$.
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Primeiramente, analisando a geometria da figura, é possível ver que temos dois triângulos congruentes pelo critério (Lado,Ângulo,Lado). Note que, as hipotenusas são iguais a $\dfrac{L}{2}$, ambos possuem o mesmo cateto adjacente e mesmo ângulo reto.
• Analisando o ponto de aplicação da força F:
Veja que temos três forças em equilíbrio, o que significa que podemos aplicar o Teorema das Três Forças. Entretanto, por ser visualmente mais simples, podemos decompor as trações, até encontrar algo como: \begin{matrix} F = 2T\cos{60^\circ} \ \ \color{royalblue}{(1)} &,& T\sin{60^\circ} = T\sin{60^\circ}
\end{matrix}• Analisando a esfera:
Veja que novamente temos três forças em equilíbrio, além do Teorema das Três forças poderíamos ver uma soma vetorial que por o corpo estar em equilíbrio deve se formar um polígono fechado, nesse caso, um triângulo retângulo (peso e normal sendo catetos com a tração sendo a hipotenusa). Entretanto, novamente por ser visualmente mais simples, podemos decompor as forças, até encontrar algo como: \begin{matrix} R = T\cos{60^\circ} \ \ \color{royalblue}{(2)} &,&T\sin{60^\circ} = Mg \ \ \color{royalblue}{(3)}
\end{matrix}• Dividindo $(3)$ por $(2)$: \begin{matrix} \tan{60^\circ} = {{\dfrac{Mg}{R}}} &\Rightarrow& R = {{\dfrac{Mg\sqrt{3}}{3}}}
\end{matrix}• Encontrando $F$ substituindo $(2)$ em $(1)$: \begin{matrix} F = 2R &\therefore& F = 2{{\left(\dfrac{Mg\sqrt{3}}{3}\right)}}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

