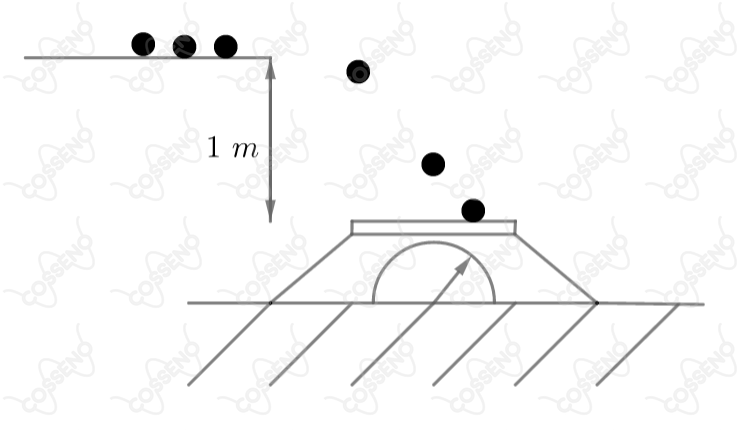
No dispositivo da figura, bolas de gude de cada uma estão caindo, a partir do repouso, de uma altura de metro, sobre a plataforma de uma balança. Elas caem a intervalos de tempos iguais praticamente paradas, sendo imediatamente retiradas da plataforma. Sabendo que o ponteiro da balança indica, em média, , e que a aceleração da gravidade vale podemos afirmar que a frequência de queda é:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Sabemos que a balança em média indica $20kg$, podemos encontrar o número de bolas sobre a balança: \begin{matrix}20kg = 20.000g &,& 20.000 = 20 \ . \ b &\Rightarrow&b = 1000 \ bolas
\end{matrix}Portanto, a cada instante temos $1000$ bolas sobre a balança, vejamos agora o tempo de queda de cada bola: \begin{matrix} \Delta H = V_o.t + a\cdot {\large{\frac{t^2}{2}}} &\Rightarrow& 1 = 0.t + 10{\large{\frac{t^2}{2}}} &\therefore& t= 5^{-1/2}s
\end{matrix}Veja que, para termos os $20kg$ em média precisamos que a frequência de queda seja $1000$ bolas a cada $5^{-1/2}s$, assim: \begin{matrix} f = {\large{\frac{1000 }{5^{-1/2}}}} = 10^3.5^{1/2} \ \color{}{\text{bolas por segundo}} \\ \\ Letra \ (D)
\end{matrix}

