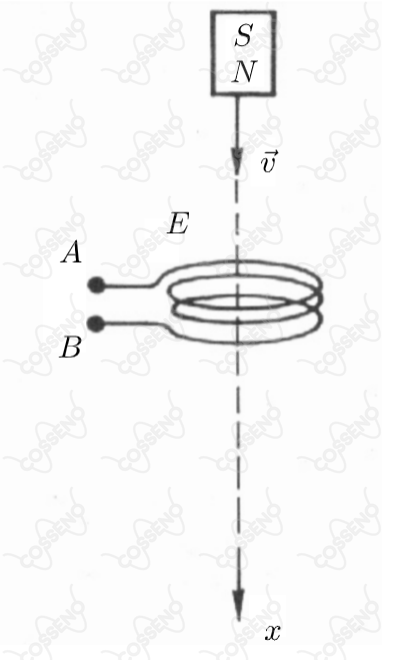
Um imã se desloca com velocidade constante ao longo do eixo da espira , atravessando-a . Tem-se que a f.e.m. induzida entre e varia em função do tempo



CossenoGPT
Teste
gratuitamente agora
mesmo! 

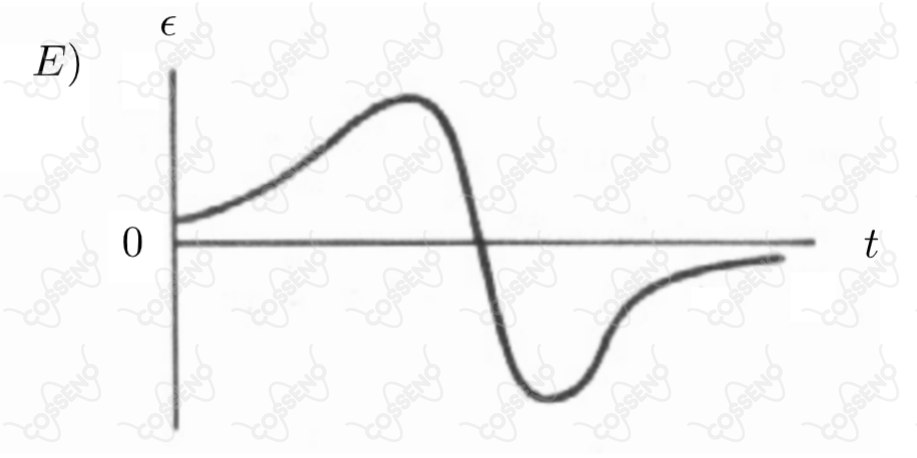
Ao aproximar o imã com seu polo norte, estaremos aumentando cada vez mais a variação de fluxo magnético na espira, esta que por sua vez irá gerar um fluxo magnético contrário, a fim de frear essa variação. Nessa perspectiva, com conhecimento da $\text{Lei de Faraday-Neumann}$, sabemos haver uma $f.m.e$ induzida $\varepsilon$ que irá aumentar conforme a variação de fluxo magnético crescer. Atente que, este processo irá ocorrer até que o imã entre na espira, no momento que o imã começar a atravessar a espira, na iminência de atravessar, não teremos mais a $f.m.e$ induzida, está que será igual a zero.
Todavia, logo após esse momento, teremos outra variação de fluxo magnético, na iminência de sair, tínhamos um fluxo interno "equilibrado" (variação nula), agora, conforme o imã for se afastando, têm-se uma variação contrária, a espira deve tentar repor a densidade de campo magnético que está "perdendo", gerando outra $f.m.e$ induzida. Obviamente, esta $f.m.e$ induzida apresentará sinal contrário a inicial (no caso, negativo), pois o fluxo gerado também será contrário.
Portanto, o único gráfico que condiz com o que analisamos é o da: \begin{matrix} Letra \ (E)
\end{matrix}

