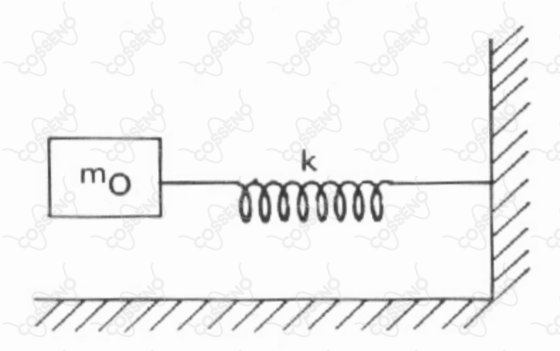
Uma forma de medir a massa de um objeto em uma estação espacial com gravidade zero é usar um instrumento como mostrado na figura. Primeiro o astronauta mede a frequência de oscilação de um sistema elástico de massa conhecida. Após, a massa desconhecida é adicionada a este sistema e uma nova medida de frequência, , de oscilação é tomada. Como podemos determinar a massa desconhecida a partir dos dois valores de medida da frequência?
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A frequência de um sistema massa mola, envolvendo uma massa $m_0$ e mola de constante $k$, é dada por:
$$f=\sqrt{\dfrac{k}{m}}$$
Dessa forma, sabemos do enunciado que:
$$f_0=\sqrt{\dfrac{k}{m_0}}\Longrightarrow k=f_0^2m_0\ \ \text{e} \ \ f=\sqrt{\dfrac{k}{m_0+m}}$$
Portanto,
$$f^2(m_0+m)=k\Longrightarrow f^2(m_0+m)=f_0^2m_0\ \therefore$$
$$m=m_0[(f_0/f_1)^2-1]$$
$$Letra\ C$$

