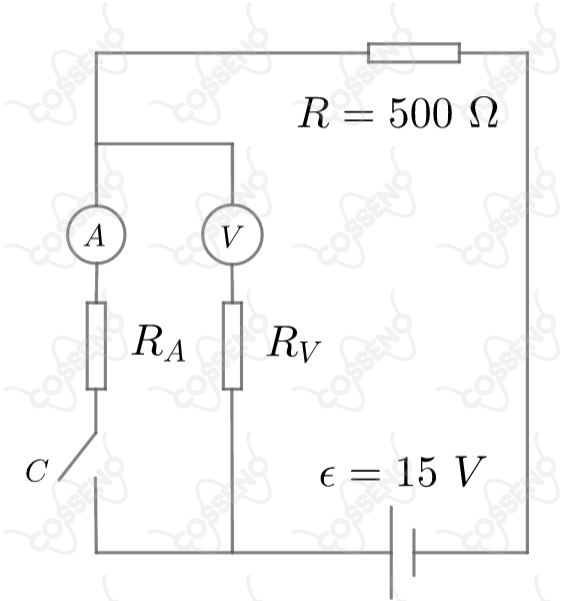
No circuito ao lado e são um voltímetro e um amperímetro respectivamente, com fundos de escala (leitura máxima) e ; e . Ao se abrir a chave :
CossenoGPT
Teste
gratuitamente agora
mesmo! 

A priori, analise o circuito fechado, quase não há passagem de corrente no voltímetro, veja pela associação das resistências em paralelo $(R_{eq})$: \begin{matrix} R_{eq} = \dfrac{5.1000}{5+1000} \approx 5 \ \Omega
\end{matrix}Fazendo a associação em série, e aplicando $\text{Primeira Lei de Ohm}$: \begin{matrix} R_T = R_{eq} + R&,& \epsilon = R_T.i_1 &\therefore& i_1 \approx 0,03 \ A
\end{matrix} Analisando agora o circuito aberto, é simples inferir que não passará correte no amperímetro, isto é, ele não registrará corrente. Nessa perspectiva, temos outro circuito, este composto pelas resistências em série, $R_V$ e $R$, logo, têm-se:\begin{matrix} \epsilon = (R_V + R).i_2 &\Rightarrow& i_2 = 0,01 \ A
\end{matrix}Continuando, o voltímetro registrará \begin{matrix}\Delta V = R_V.i_2 &\therefore& \Delta V = 10 \ V
\end{matrix}Portanto, $\text{o voltímetro terá leitura maior que 1 V e pode se danificar}$. \begin{matrix} Letra \ (E)
\end{matrix}

