A priori, pode-se imaginar o tronco do cilindro de raio $r$ como: 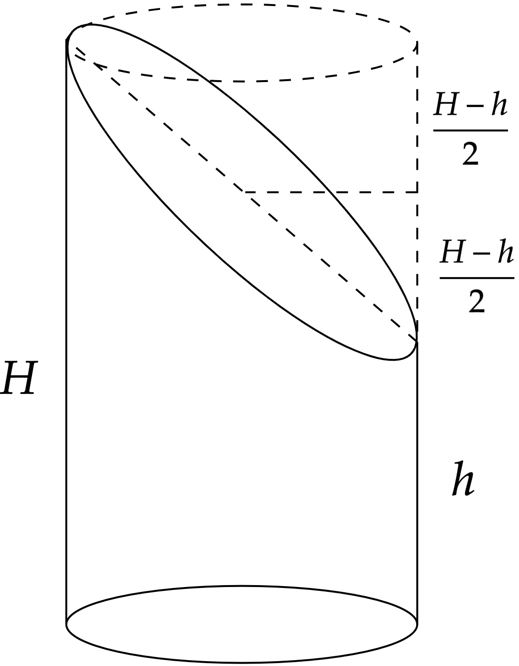Nessa perspectiva, atente que o volume do cilindro será o volume do cilindro menor de altura $h$, e metade do cilindro restante de altura $H-h$: \begin{matrix} V_i = \pi r^2 h \ + \ {{\dfrac{1}{2}}}\pi r^2 (H-h)&\therefore& V_i = \pi r^2 {{(\dfrac{H+h}{2})}} \end{matrix}Continuando, ao dobrar a base menor temos um novo volume $V$, este volume é um terço maior que o original, logo, analogamente: \begin{matrix} V = V_i + {{\dfrac{V_i}{3}}} = {{\dfrac{4V_i}{3}}} &\Rightarrow& \pi r^2 {{ \left(\dfrac{H+2h}{2} \right)}} = {{\dfrac{4}{3}}} \cdot \pi r^2 {{ \left(\dfrac{H+h}{2}\right) }} \end{matrix}Assim, \begin{matrix} 3(H+2h) = 4(H+h) &\therefore& H = 2r & \tiny{\blacksquare} \end{matrix}\begin{matrix} Letra \ (B) \end{matrix}