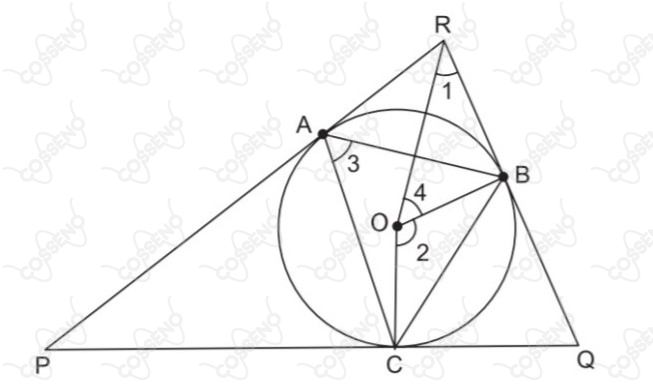
Considere o triângulo ao lado, circunscrito a uma circunferência de centro , cujos pontos de tangência são , e . Sabe-se que os ângulos , e estão, nesta ordem, em progressão aritmética de razão . Os ângulos , , , conforme mostrado na figura abaixo medem, nesta ordem:
CossenoGPT
Teste
gratuitamente agora
mesmo! 

Ângulos em progressão:\begin{matrix} \hat{P} + \hat{Q} + \hat{R} = 180º \ \Rightarrow \ \hat{P} + (\hat{P} + 20º) + (\hat{P} + 40º) = 180º \\
\end{matrix}\begin{matrix} \hat{P} = 40º &,& \hat{Q} = 60º &,& \hat{R} = 80º
\end{matrix}$\text{Ângulo}$ $\hat{1}$: Perceba que, pelos $\text{Segmentos Tangentes}$, o triângulo $ARB$ é isósceles, com dois ângulos iguais a $50º$. Com isso, os dois triângulos de $ARB$ são congruentes por $\text{L.A.L}$, assim:
\begin{matrix} \hat{1} + \hat{1} = 80º \ \Rightarrow \ \fbox{$\hat{1} = 40º $}
\end{matrix}$\text{Ângulo}$ $\hat{2}$: Novamente, pelos $\text{Segmentos Tangentes}$, o triângulo $BCQ$ é isósceles, além de que, o triângulo $BCO$ também é isósceles $(\overline{BO} = \overline{OC} = R )$. Dessa forma, é fácil perceber que, traçando $\overline{OQ}$, teremos dois triângulos retângulos congruentes $(\text{L.A.L})$, inclusive, $\overline{OQ}$ é bissetriz, assim: \begin{matrix} \hat{2} = C\hat{O}Q + B\hat{O}Q \ \Rightarrow \ \hat{2} = 60º + 60º \\ \\ \fbox{$\hat{2} = 120º $}
\end{matrix}$\text{Ângulo}$ $\hat{3}$: Veja que, o $\hat{3}$ é o ângulo inscrito de $\hat{2}$, assim:
\begin{matrix} \hat{3} = \dfrac{\hat{2}}{2} & \Rightarrow & \fbox{$\hat{3} = 60º $}
\end{matrix}$\text{Ângulo}$ $\hat{4}$: O triângulo $BOR$ é retângulo, como já conhecemos o ângulo $\hat{1}$, temos: \begin{matrix} \hat{4} = 180º - ( \hat{1} + 90º) &\therefore& \fbox{$\hat{4} = 50º $}
\end{matrix}\begin{matrix}Letra \ (A)
\end{matrix}

