O enunciado induz ao trabalho com a forma geométrica dos números complexos, nesse caso em questão, podemos visualizar a situação: 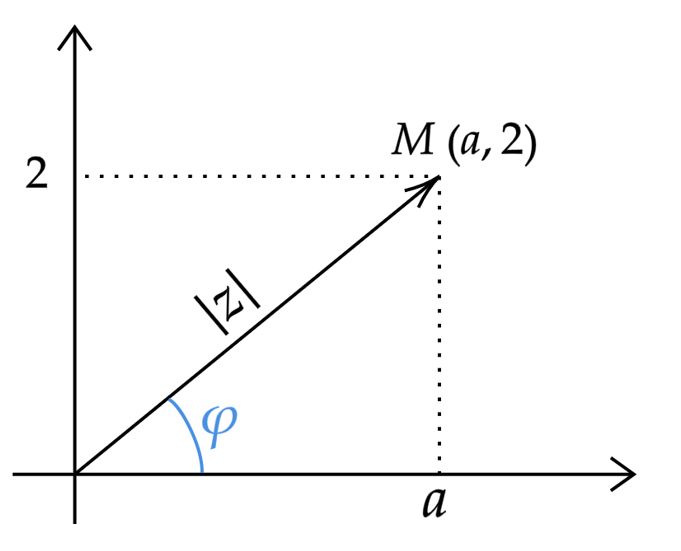Agora, podemos representar $z$ numa forma polar:\begin{matrix} z = |z| \ . \ (\cos{\varphi} + i\sin{\varphi}) \\ \Downarrow \\ z^6 = |z|^6 \ . \ (\cos{6\varphi} + i\sin{6\varphi}) \ \ , \ \ z^6 \in \mathbb{R} \\ \Downarrow \\ \sin{6\varphi} = 0 \ \ \Rightarrow \ \ 6\varphi = k\pi \ \ , \ \ k = 1,2,...,6 \\ \Downarrow \\ {\varphi_1 =\dfrac{\pi}{6}} \ \ \ , \ \ \ \varphi_2 = {\dfrac{\pi}{3}} \end{matrix}$\color{orangered}{Obs:}$ Note que, $\varphi_3$ em diante não satisfaz o problema, visto que o argumento $(\varphi)$ está em $(0, \pi/2)$. Repare novamente na figura, podemos encontrar $a$ fazendo: \begin{matrix} \tan{\varphi} = {\dfrac{2}{a}} &\Rightarrow& a = {\dfrac{2}{\tan{\varphi}}} \\ \\ a_1 = {\dfrac{2}{\tan{\varphi_1}}} &,& a_2 = {\dfrac{2}{\tan{\varphi_2}}} \\ \\ \fbox{$a_1 = {\dfrac{6}{\sqrt{3}}}$} &,& \fbox{$a_2 = {\dfrac{2}{\sqrt{3}}} $} \end{matrix} \begin{matrix} \fbox{$a_1 \ . \ a_2 = 4$} \\ \\ Letra \ (A) \end{matrix}

Utilizando o triângulo de Pascal para abrir o binômio: $$(a+2i)^{6}=(a^{6}-60a^{4}+240a^{2}-64)+i(12a^{5}-160a^{3}+192a)$$ Para que $(a+2i)$ seja real, o termo que multiplica o "i" deve ser zero. Sendo assim, os termos do conjunto S são as raíses da expressão que multiplica o "i". Basta então descobrir as raíses e multiplicá-las. Mas, lembre-se que $a>0$ uma vez que o argumento de z está contido no primeiro quadrante. $$12a^{5}-160a^{3}+192a=0 ⇒ a(3a^{4}-40a^{2}+48)=0$$ Note que zero é solução, o que nos levaria a "nenhuma das anteriores" ou "n.d.a", porém, vamos resolver ignorando essa raís: $$a={-2\sqrt{3}, 2\sqrt{3}, -\frac{2}{\sqrt{3}}, \frac{2}{\sqrt{3}}}$$ Como já foi dito, z está no primeiro quadrante, logo $a>0$. Multiplicando somente os positivos encontramos a resposta $4$.